Modelli probabilistici di fenomeni aleatori

La teoria della probabilità si occupa dello studio dei fenomeni aleatori. Quando non siamo in grado di dare una caratterizzazione esatta del fenomeno e dobbiamo dare una descrizione globale del fenomeno stesso, usiamo la probabilità.

Probabilità e statistica

Esperimenti aleatori

Sono aleatori tutti gli esperimenti per i quali è difficile o impossibile prevedere in modo esatto il risultato, ma presentano una qualche forma di regolarità. Il comportamento dei fenomeni aleatori può essere descritto solo attraverso grandezze globali e/o medie.

Non ci interessa solo il caso in cui sia impossibile, ma anche sia molto difficile, così tanto da rendere la descrizione irrealizzabile.

Pensando alla definizione di probabilità, i valori medi possono essere i momenti e le regolarità del primo o second'ordine. Tanto per dare un esempio, è difficile predire esattamente il risultato di ogni lancio del dado, ma se il dado non è truccato posso dire che ogni faccia ha la stessa probabilità di uscire. Posso prevedere il valor medio del risultato e la statistica collegata.

Teoria della probabilità e statistica

La teoria della probabilità si occupa della costruzione di modelli probabilistici (matematici) che descrivano i fenomeni aleatori. La statistica, invece, si occupa di verificare l'aderenza di un modello rispetto ai dati sperimentali.

Nella parte di teoria della probabilità possiamo dire qual è la funzione di densità di probabilità del dado. La statistica si preoccupa di dire se, dato un dado, questo aderisce al modello della teoria della probabilità o se questo è truccato. Gli ambiti in cui viene utilizzata la teoria della probabilità sono molti, per esempio:

• teoria delle code;
• instradamento ottimo dei pacchetti;
• analisi fatta a livello statistico;
• meccanica statistica relativa ai gas (posso descrivere la pressione, che è un valore medio, e non la posizione di ogni molecola);
• elaborazione e trasmissione dell'informazione.

Teoria dell'informazione

La teoria dell'informazione studia i problemi legati all'elaborazione e alla trasmissione dell'informazione utilizzando un approccio probabilistico.

Esempio:

Se dico:

1. oggi il treno per Milano delle 17.25 sarà in ritardo di 10 minuti
2. oggi il treno per Milano delle 17.25 sarà puntuale

Pensando a come funzionano le ferrovie in Italia, qual è l'informazione più importante? La seconda, perché si verifica raramente: un evento raro è molto più informativo. La misura di informazione è basata sulla probabilità. L'informazione associata ad un evento è inversamente proporzionale alla sua probabilità di occorrenza.

L'informazione si misura con la definizione

$i(m_{k})=\log {\frac {1}{p(m_{k})}}$

Dall'informazione $i(m)$ si passa alla definizione di entropia:

$H(M)=\sum _{k=i}^{m}p(m_{k})\cdot i(m_{k})=\sum _{k=i}^{m}p(m_{k})\cdot \log {\frac {1}{p(m_{k})}}=E[i]{\text{ con }}m_{k}\in M$

L'entropia non è altro che l'informazione media di una sorgente.

Esempio:

Supponiamo di avere una sorgente $X$ che emette simboli 0 e 1. La sorgente emette simboli in modo equiprobabile, quindi

• $p(0)=1/2$
• $p(1)=1/2$

Di solito si hanno delle stringhe di bit 1101110011. Un'operazione importante è la codifica della sorgente; quello che si vuole fare è trovare un codice per rappresentare questa stringa, con o senza perdita, con un numero minore di bit. Con la probabilità data non è possibile comprimere la stringa, perché i simboli sono equiprobabili. Se i simboli sono indipendenti, il fatto che sia uscito un 1 o uno 0 non influenza il risultato del prossimo simbolo.

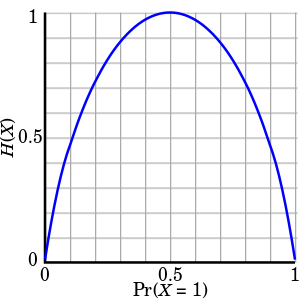
Al contrario, se i bit non sono equiprobabili, posso rappresentare con meno bit i simboli della sorgente, posso comprimere.

La costruzione di modelli semplificati può cambiare nettamente le prestazioni di un canale o di un sistema di telecomunicazioni.

Statistica

Definizione: Fenomeno aleatorio

Un fenomeno aleatorio è un esperimento i cui possibili risultati appartengono ad un insieme ben definito e dove l'esito non è prevedibile (o predicibile) a priori. È importante che l'insieme dei possibili risultati sia ben definito, deve essere noto.

Definizione: Spazio degli esiti

Lo spazio degli esiti, o spazio campione $\Omega$ associato ad un esperimento aleatorio, è l'insieme di tutti i possibili risultati di un esperimento. Può essere finito o infinito, sia numerabile che non numerabile.

Definizione: Evento

Dato uno spazio campione $\Omega$, si dice evento un qualsiasi sottoinsieme A di $\Omega$, $A\subseteq \Omega$.

Esempio:

Si consideri il lancio di un dado a 6 facce. Si ha:

$\Omega =\left\{1,2,3,4,5,6\right\}$

Definizione: Spazio degli eventi

Dato uno spazio campione $\Omega$, si definisce spazio degli eventi F l'insieme non vuoto che contiene tutti gli elementi di interesse (determinabili su $\Omega$) che soddisfano le seguenti proprietà:

1. $\Omega ,\varnothing \in F$
2. $A,B\in F\Rightarrow A\cap B\in F$ (dai teoremi di De Morgan)
3. $\forall A\subseteq F\Rightarrow {\overline {A}}\subseteq F$

Un spazio F è una $\sigma$-algebra se vale anche:

• $U_{i=1}^{k}A\in F\ \forall A_{1},\cdots ,A_{k},\ k\in [1,\infty ]$

cioè, se si ha chiusura rispetto all'unione numerabile. Noi useremo esclusivamente $\sigma$-algebre.

Ci saranno, in generale, più di uno spazio F degli eventi. Il più banale deve contenere l'unione ed il complemento degli eventi.

$F_{1}=\left\{\varnothing ,\Omega \right\}$

Esempio: Esempio di utilizzo della teoria della probabilità: il cut detection

In un filmato, si assume che frame vicini siano simili tra loro. Qual è l'interframe, la distanza tra due frame? Quando l'interframe è troppo elevato, posso dichiarare che c'è stata una transizione del filmato. Posso usare soglie fisse o non fisse (le soglie adattative). Grazie al modello probabilistico, si può introdurre la soglia adattativa, cioè che si adatta in base al modello di probabilità che stimo sui dati.

Insieme delle parti

Definizione: Insieme delle parti

Si dice insieme delle parti lo spazio degli eventi F che contiene tutti i possibili eventi di $\Omega$, cioè tutti i possibili sottoinsiemi che posso costruire con gli elementi di $\Omega$.

$F_{2}=P(\Omega )=2^{\Omega }$

Esempio: I dadi

L'insieme delle parti è

$F_{2}=\left\{\varnothing ,\{1\},\{2\},\{1,3,5\},\{2,4,6\},\{1,2,3\},\cdots ,\Omega \right\}$

Classe di insiemi

Definizione: Classi di insiemi

Dato un insieme X si dice classe C una collezione di sottoinsiemi di X. La classe di tutti i possibili sottoinsiemi di X si chiama insieme (o collezione, o classe) delle parti.

Definizione: Partizione di un insieme

Una partizione è la classe di sottoinsiemi $\{X_{1},X_{2},\cdots ,X_{n}\}$ tali che

• $X_{i}\cap X_{j}=\{\varnothing \}\ \forall i\neq j$
• $\sum _{i=1}^{n}X_{i}=X$

Esempio: Il dado

Con $\Omega =\{1,2,3,4,5,6\}$, una partizione può essere

$P=\{(1,3),(2,4),(5,6)\}$

Definizione: Cardinalità

La cardinalità di un insieme è il numero di elementi che esso contiene. Se la cardinalità di $\Omega$ è N, allora la cardinalità dell'insieme delle parti F è

$|F|=2^{N}$

Definizioni di probabilità

Probabilità secondo la frequenza relativa

Una delle possibili definizioni di probabilità è quella che usa la frequenza relativa. Si dice che la probabilità $P(A)$ di un evento A è data da

$P(A)=\lim _{n\rightarrow \infty }{\frac {n_{A}}{n}}$

dove n è il numero di volte che si ripete l'esperimento, mentre $n_{A}$ è il numero di volte che si verifica l'evento A.

Probabilità secondo il modello probabilistico

Un modello probabilistico di un fenomeno aleatorio è lo spazio di probabilità identificato da tre elementi $(\Omega ,F,P)$, dove:

• $\Omega$ è lo spazio degli esiti;
• F è lo spazio degli eventi;
• P è la probabilità.

Definizione: Probabilità $P$

Assegnato uno spazio campione $\Omega$ ed una $\sigma$-algebra F di eventi di $\Omega$, si definisce probabilità una funzione P definita su F a valori in $\mathbb {R}$ (non negativi), tale che

1. $P(A)\geq 0$
2. $P(\Omega )=1$
3. se $\left\{A_{n}\right\}_{n=1}^{+\infty }$ è una successione di eventi mutuamente esclusivi, cioè

$(A_{i})\cap A_{j}=\varnothing \ \forall i\neq j{\text{, allora }}P\left(\bigcup _{i}^{\infty }\right)=\sum _{i=1}^{\infty }P(A_{i})$

Quest'ultima proprietà è detta additività numerabile, perché indica che gli elementi hanno intersezione nulla e la somma delle loro probabilità si può portare fuori dal segno di probabilità.

Note