Esempi di processi stocastici Processi PAM Processi gaussiani Processi di Markov

Processi e catene di Markov

Cominciamo col capire cosa sono le catene di Markov. Prendiamo un meteo, in cui si hanno soltanto due stati:

• sole, $S$;
• nuvoloso, $N$.

Se oggi c'è il sole, allora domani ci sarà

• sole con probabilità ${\frac {1}{3}}$;
• nuvoloso con probabilità ${\frac {2}{3}}$.

Al contrario, se oggi è nuvoloso, allora domani ci sarà

• sole con probabilità ${\frac {1}{2}}$;
• nuvoloso con probabilità ${\frac {1}{2}}$.

Questa è una catena di Markov. Il tempo di domani dipende dal tempo di oggi, e non dal tempo di ieri; inoltre, la probabilità che esce da ogni stato è unitaria, quindi anche la probabilità che in un dato istante si sia in un determinato punto soddisferà anch'essa la proprietà di uniterietà.

Definizione: Processo di Markov

Il processo $\{X(t),t\in T\}$ è un processo di Markov se

$P(X(t_{n})|X(t_{n-1}),X(t_{n-2}),\cdots x(t_{1}))=P(X(t_{n})|X(t_{n-1}))\ \forall t_{1}<t_{2}<\cdots <t_{n}\in T$

In altre parole, possiamo scrivere che una variabile casuale $X(t_{n})$ dipende solo dalla variabile casuale $X(t_{n-1})$, mentre è indipendente da tutte le variabili casuali precedenti l'istante $t_{n-1}$.

Implicazioni:

1. la probabilità del futuro, dato passato e presente, dipende solo dal presente.
2. la probabilità del futuro, congiunta a quella del passato e conoscendo il presente, è

$P({\text{futuro}}|{\text{passato}},{\text{presente}})=P({\text{futuro}}|{\text{presente}})\cdot P({\text{presente}}|{\text{passato}})$

Gli eventi che soddisfano questa seconda condizione sono detti condizionalmente indipendenti, cioè sono indipendenti soltanto se vi è la conoscenza dello stato intermedio. Nel caso in cui non si conosca il presente, allora passato e futuro non sono più indipendenti.

Densità di probabilità del processo di Markov

• $f_{X(t_{n})|X(t_{n-1})\cdots X(t_{1})}(x_{n}|x_{n-1},x_{n-2}\cdots x_{1})=f_{X(t_{n})|X(t_{n-1})}(x_{n}|x_{n-1})$
• $\left\{{\begin{aligned}&f_{X(t_{n})X(t_{n-1})\cdots X(t_{1})}(x_{n},x_{n-1},\cdots ,x_{1})=\\&=f_{X(t_{n})|X(t_{n-1}),X(t_{n-2})\cdots X(t_{1})}(x_{n}|x_{n-1},x_{n-2}\cdots x_{1})\times \cdots \times f_{X(t_{2})|X(t_{1})}(x_{2}|x_{1})\times f_{X(t_{1})}(x_{1})\\&=f_{X(t_{n})|X(t_{n-1})}(x_{n}|x_{n-1})\times \cdots \times f_{X(t_{2})|X(t_{1})}(x_{2}|x_{1})\times f_{X(t_{1})}(x_{1})\\&=\left[\Pi _{k=1}^{n-1}f_{X(t_{k+1})|X(t_{k})}(x_{k+1}|x_{k})\right]\cdot f_{X(t_{1})}(x_{1})\end{aligned}}\right.$

Per caratterizzare una catena di Markov è sufficiente conoscere la densità di probabilità del second'ordine, non serve scendere fino all'$n$-esimo ordine. In questo modo, la trattazione diventa molto più semplice, fino a renderla quasi banale.

Classificazione

I processi di Markov si possono classificare in base allo stato/tempo continuo/discreto:

• stato continuo e tempo continuo: processo a tempo continuo;
• stato continuo e tempo discreto: processo a tempo discreto;
• stato discreto e tempo continuo: catena a tempo continuo;
• stato discreto e tempo discreto: catena a tempo discreto.

Catene di Markov a tempo discreto

Si ha

• $T=\{0,1,\cdots \}$
• $S=\{1,2,\cdots \}$

che sono due insiemi discreti. La catena di Markov è caratterizzata da due quantità:

• la probabilità incondizionata

$P_{i}=P\left(X(n)=i\right)$

• la matrice delle probabilità di transizione $P_{ij}(m,n)=P(X(n)=j|X(m)=i)$.

Si ha

$P_{i}(n)\in [0,1]\ \forall i\in S,\forall n\in T\ |\ \sum _{i\in S}P_{i}(n)=1$

cioè, per ogni istante, la somma delle probabilità di tutti gli stati è unitaria; noto l'alfabeto $s$, la probabilità incondizionata si può scrivere come

${\underline {P}}(n)=[P_{1}(n)\ P_{2}(n)\ \cdots \ P_{|s|}(n)]$

La stessa condizione si può esprimere con

${\underline {P}}\cdot e^{T}=1\ e=[1\ 1\ \cdots \ 1]$

Fissati due istanti temporali $n<m$ e dato lo stato di partenza $n$, la somma delle probabilità degli stati di arrivo è unitaria.

${\underline {P}}(m,n)=\left[{\begin{matrix}P_{1,1}(m,n)&P_{1,2}(m,n)&\cdots &P_{1,|s|}(m,n)\\P_{2,1}(m,n)&P(2,2)(m,n)&\cdots &P_{2,|s|}(m,n)\\\vdots &\vdots &\ddots &\vdots \\P_{|s|,1}(m,n)&P_{|s|,2}(m,n)&\cdots &P_{|s|,|s|}(m,n)\end{matrix}}\right]$

dove la somma dei valori di ogni singola riga è $1$

$\sum _{i=1,2,\cdots |s|}P_{i,j}(m,n)=1\ \forall j\in [0,1,\cdots |s|]$

${\underline {P}}(m,n)\cdot e^{T}=e^{T}=[1\ 1\ \cdots \ 1]$

Per ogni coppia $m,n$, il valore di ${\underline {P}}(m,n)$ sarà diverso. Si ha

${\underline {P}}(n)={\underline {P}}(m,n)\cdots {\underline {P}}(m)$

${\begin{aligned}P_{i,j}(m,n)&=P(X(n)=j|X(m)=j)\\&=\sum _{l\in S}P(X(n)=j|X(u)=l,X(m)=i)\cdot P(X(u)=l|X(m=i))\\&=\sum _{l\in S}P_{l,j}(u,n)\cdot P_{i,l}(m,n)\end{aligned}}$

Quest'ultima è detta l'equazione di Chapman e Kolmogorov, che in forma matriciale si può scrivere come

${\underline {P}}(m,n)={\underline {P}}(m,u)\cdot {\underline {P}}(u,n)$

da cui si ha

${\underline {P}}(m,n)=\prod _{k=m}^{n-1}{\underline {P}}(k,k+1)$

Per caratterizzare una catena di Markov, basta conoscere:

• ${\underline {P}}(0)$
• ${\underline {P}}(k,k+1)\ \forall k\in T$
• ${\underline {P}}(n)={\underline {P}}(0)\cdot {\underline {P}}(0,1)\cdot {\underline {P}}(1,2)\cdots {\underline {P}}(n-1,n)$

Esempio: Caso 1

Si ha

${\underline {P}}(1)={\underline {P}}(0)\cdot {\underline {\underline {P}}}=[1\ 0]\cdot \left[{\begin{matrix}0&1\\1&0\end{matrix}}\right]=[0\ 1]$

${\underline {P}}(2)={\underline {P}}(0)\cdot {\underline {\underline {P}}}^{2}=[1\ 0]\cdot \left[{\begin{matrix}0&1\\1&0\end{matrix}}\right]\cdot \left[{\begin{matrix}0&1\\1&0\end{matrix}}\right]=[1\ 0]$

La sequenza degli stati è deterministica,

• $P(2m)=[1\ 0]\ \forall m\in \mathbb {N}$
• $P(2m+1)=[0\ 1]\ \forall m\in \mathbb {N}$

Esempio: Caso 2

Si ha

${\underline {\underline {P}}}=\left[{\begin{matrix}0&1\\1&0\end{matrix}}\right]$

$P(0)=\left[{\frac {1}{2}}\ {\frac {1}{2}}\right]$

da cui

${\underline {P}}(1)={\underline {P}}(0)\cdot {\underline {\underline {P}}}=\left[{\frac {1}{2}}\ {\frac {1}{2}}\right]$

${\underline {P}}(2)={\underline {P}}(0)\cdot {\underline {\underline {P}}}^{2}=\left[{\frac {1}{2}}\ {\frac {1}{2}}\right]$

da cui si deduce che vale

${\underline {P}}(m)=\left[{\frac {1}{2}}\ {\frac {1}{2}}\right]\ \forall m\in T$

Definizione: Catena di Markov omogenea

Una catena di Markov è detta omogenea se

${\underline {P}}(k,k+1)={\underline {\underline {P}}}\ \forall k\in T$

ossia, la matrice di probabilità di transizione ad un passo $(k,k+1)$ è la stessa per tutti i $k\in T$.

Esempio:

Si ha

${\underline {\underline {P}}}=\left[{\begin{matrix}P_{11}&P_{12}\\P_{21}&P_{22}\end{matrix}}\right]$

da cui

• ${\underline {P}}(0)=[P_{1}\ P_{2}]$
• $s=\{1,2\}$
• $T=\{0,1,\cdots \}$

Definizione: Distribuzione stazionaria

Data una catena di Markov omogenea, si definisce distribuzione stazionaria il vettore di probabilità

${\underline {\Pi }}=[\pi _{1}\ \pi _{2}\ \cdots \ \pi _{|s|}]$

tale che

• ${\underline {\Pi }}\cdot {\underline {\underline {P}}}={\underline {\Pi }}$
• ${\underline {\Pi }}\cdot e^{T}=1$

da cui, nel caso in cui $P(0)={\underline {\Pi }}$, allora si ottiene

$P(n)={\underline {\Pi }}\ \forall n\in T$

In generale, una catena di Markov può avere più distribuzioni stazionarie.

Esempio:

Sia

${\underline {\underline {P}}}=\left[{\begin{matrix}0&1&0\\1&0&0\\0&0&1\end{matrix}}\right]$

da cui si ha

• $\Pi _{1}=\left[{\frac {1}{2}}\ {\frac {1}{2}}\ 0\right]$
• $\Pi _{2}=[0\ 0\ 1]$
• $\Pi _{3}=\left[{\frac {1}{4}}\ {\frac {1}{4}}\ {\frac {1}{4}}\right]$

Definizione: Catena di Markov irriducibile

Una catena di Markov si dice irriducibile se non è possibile portare la matrice di probabilità di transizione in una forma diagonale a blocchi, del tipo

$\left[{\begin{matrix}\left\{{\begin{matrix}0&1\\1&0\end{matrix}}\right\}&{\begin{matrix}0\\0\end{matrix}}\\{\begin{matrix}0&0\end{matrix}}&1\end{matrix}}\right]$

Se una catena di Markov è irriducibile, allora la distribuzione stazionaria esiste ed è unica.

Definizione: Distribuzione limite

Una distribuzione stazionaria ${\underline {\Pi }}$ si dice distribuzione limite se

$\lim _{n\to \infty }{\underline {P}}(n)={\underline {P}}$

Questo deve valere $\forall P(0)$, cioè per qualsiasi condizione iniziale.

Definizione: Catena di Markov aperiodica

Una catena di Markov omogenea ed irriducibile è aperiodica se il massimo comun divisore delle lunghezze di tutti i cammini chiusi che si possono individuare sul diagramma delle transizioni è pari a $1$.

Esempio:

Catena periodica di periodo $3$:

In questo caso, $MDC=3$.

Esempio:

Catena di Markov aperiodica:

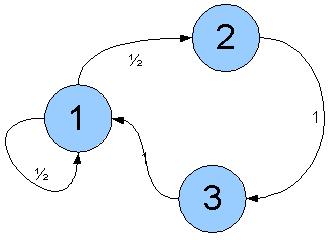
In questo caso, $MDC=1$.

Se una catena di Markov omogenea ed irriducibile è aperiodica, allora la distribuzione stazionaria è anche distribuzione limite. Per queste catene di Markov, a regime la probabilità assoluta è indipendente dal tempo, dando origine a processi stazionari.

Nota: una distribuzione ${\underline {\Pi }}$ è una distribuzione limite se

$\lim _{n\to \infty }{\underline {\underline {P}}}^{n}=\left[{\begin{matrix}{\underline {\Pi }}\\{\underline {\Pi }}\\{\underline {\Pi }}\end{matrix}}\right]$

Definizione: Matrice doppiamente stocastica

Una matrice di probabilità di transizione è doppiamente stocastica se la somma degli elementi di ciascuna colonna è unitario; in tal caso, la distribuzione limite risulta essere

${\underline {\Pi }}=\left[{\frac {1}{|s|}}\ {\frac {1}{|s|}}\ \cdots \ {\frac {1}{|s|}}\right]$

Esempio:

Si ha

• ${\underline {\underline {P}}}=\left[{\begin{matrix}{\frac {1}{4}}&{\frac {1}{4}}&{\frac {1}{2}}\\{\frac {1}{4}}&{\frac {1}{4}}&{\frac {1}{2}}\\{\frac {1}{2}}&{\frac {1}{2}}&0\end{matrix}}\right]$
• ${\underline {\Pi }}=[{\underline {\pi _{1}}}\ {\underline {\pi _{2}}}\ \cdots \ {\underline {\pi _{3}}}]$

da cui

$\left\{{\begin{matrix}{\underline {\Pi }}\cdot {\underline {\underline {P}}}={\underline {\Pi }}\\{\underline {\Pi }}\cdot {\underline {e}}^{T}=1\end{matrix}}\right.$

$\left\{{\begin{aligned}{\frac {1}{4}}\pi _{1}+{\frac {1}{4}}\pi _{2}+{\frac {1}{2}}\pi _{3}&=\pi _{1}\\\cdots &=\pi _{2}\\{\frac {1}{2}}\pi _{1}+{\frac {1}{2}}\pi _{2}&=\pi _{3}\\\pi _{1}+\pi _{2}+\pi _{3}&=1\end{aligned}}\right.$

si ottiene

${\underline {\Pi }}=\left[{\frac {1}{3}}\ {\frac {1}{3}}\ {\frac {1}{3}}\right]$

che è una matrice stocastica.