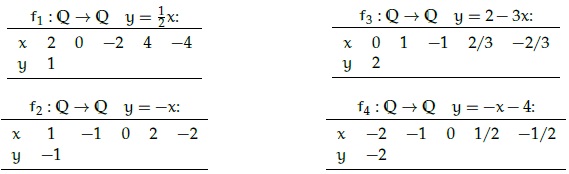Esercizi sulle funzioni (superiori)

I seguenti esercizi riguardano Le Funzioni studiati nella Lezione 8. Essi sono divisi per paragrafi in modo tale da favorire la scelta degli esercizi specifici.

Funzioni

ESERCIZIO 1. È vero che la corrispondenza che associa ad ogni regione italiana il suo capoluogo di provincia è una funzione?

• A. Completa: D = I.D. =................................................................;
• B. è vero che IM. = {città d’Italia}?
• C. completa f(Liguria) =........................; f(........................) = Cagliari?

ESERCIZIO 2. Assegnati gli insiemi A = fmare, ruspa, fegato, generaleg e B = {1, 2, 3, 4, 5, 6, 7, 8, 9} la corrispondenza che associa ad ogni elemento di A il numero di lettere di cui è composta la parola è una funzione?

• A. Rappresentala con grafico sagittale e stabilisci l’insieme immagine;
• B. quale relazione sussiste tra B e IM.?

ESERCIZIO 3. Quali tra le seguenti relazioni sono funzioni?

ESERCIZIO 4. Si è ammessi a una facoltà universitaria se nel test d’ingresso si è avuto un punteggio compreso tra 60 incluso e 100 incluso. La corrispondenza che associa ad ogni studente che ha superato il test il punteggio ottenuto è una funzione? Se sì di che tipo è la funzione?

ESERCIZIO 5. Spiega perché la funzione che associa a ciascuna persona il suo codice fiscale è biunivoca.

Funzioni tra insiemi numerici

ESERCIZIO 6. Nella corrispondenza che associa ad ogni intero il suo valore assoluto (ESEMPIO 5 DELLA LEZIONE 8), è vero che scelto un qualunque numero naturale è possibile determinare almeno un numero intero di cui è immagine? Completate: f(......) = 45. L’osservazione precedente permette di concludere che tale funzione è suriettiva? Fate la rappresentazione sagittale della funzione.

ESERCIZIO 7. Data la funzione y = x - 2 con dominio N - {0, 1} e codominio N completa l’analisi dell’ESEMPIO 7 DELLA LEZIONE 8:

• A. elementi diversi del dominio hanno immagini diverse, quindi tale funzione è iniettiva; si ha anche IM. = C = N e pertanto la funzione è suriettiva, quindi ..................;
• B.' preso y = 8 sapresti trovare l’elemento del dominio di cui è immagine? ..............;

ESERCIZIO 8. Stabilisci se la funzione f : y = 1/x è iniettiva. Nell’insieme immagine c’è lo zero? Completate C = IM. = ... Completate la tabella

ESERCIZIO 9. Consideriamo la funzione f che associa ad ogni numero razionale il suo triplo.

Q -f-> Q; la sua espressione in forma analitica è f : y = .........

D = I.D. = Q; possiamo moltiplicare per 3 qualunque numero razionale.

C = IM. = Q; infatti per ogni numero razionale y c’è un numero razionale x di cui y è il triplo, basta dividere y per 3.

• A. qual è l’immagine di 0? ...............................................................
• B. quale elemento del dominio ha per immagine 5?' ...............................................................
• C. è vero che ogni numero positivo ha l’immagine positiva? ...............................................................
• D. è vero che -1 è immagine di -3? ...............................................................
• E. la funzione è iniettiva? ...............................................................
• F. la funzione è biunivoca? ...............................................................

Fai il grafo sagittale della funzione.

ESERCIZIO 10. Per ciascuna delle seguenti funzioni determinare l’insieme di definizione, l’insieme immagine e stabilire se la funzione è iniettiva o suriettiva.

• A. f : Z --> Z, x --> 2x;
• B. f : Z --> Z, x --> x²;
• C. f : N --> N, x --> 1/x;
• D. f : Q --> Q, x --> 2x;
• E. f : Q --> Q, x --> 1/x.

ESERCIZIO 11. Per ciascuna delle funzioni di seguito elencate, da R in R, riempite le colonne della tabella.

EZECIZIO 12. Assegnata la funzione f : Q --> Q, definita da y = x² + 1 non è né iniettiva, né suriettiva. Motiva questa affermazione scegliendo gli opportuni valori di x e di y.

Composizione di funzioni

ESERCIZIO 13. Date le funzioni f(x) = 2x + 1 e g(x) = 3x + 2 che hanno per dominio rispettivamente A = {x ∈ Z | -2 ≤ x ≤ 2|, B = {x ∈ Z | -1 ≤ x ≤ 3|. Scrivi le espressioni analitiche delle funzioni f o g e g o f.

ESERCIZIO 14. Date le seguenti funzioni f cerca due funzioni g e h tali che g o h = f.

ESERCIZIO 15. Date le funzioni f e g determina le funzioni composte richieste.

ESERCIZIO 16. Date le funzioni f e g determina le funzioni composte richieste.

La retta e gli insiemi numerici

ESERCIZIO 17. Determina sulla retta reale i punti immagine dei seguenti numeri reali: α = 3/2 √2; β = 2/5 + 1/√2 ; δ = - (√3 + √2); λ = √3 - 3.

ESERCIZIO 18. Verifica che il numero χ = √3 + √2 non è uguale al numero ω = √5, usando la rappresentazione sulla retta orientata.

ESERCIZIO 19. Stabilisci il valore di verità della proposizione: “poiché tra 2 e 3 non vi è nessun altro numero naturale, anche tra √2 e √3 non vi è nessun numero reale”.

Il metodo delle coordinate cartesiane

'ESERCIZIO 20. Per ciascuna coppia di punti indica in quale quadrante si trova, se si trova su un asse indica l’asse: (0; -1), (3/2; -5/4), (0; 13), (5/3; 1), (1; -5/3), (-8; 9), (-2; -14), (-1; 0). Completa l’osservazione conclusiva:

• tutte le coppie del tipo (+; +) individuano punti del .........;
• tutte le coppie del tipo (...; ...) individuano punti del IV quadrante;
• tutte le coppie del tipo (-; +) individuano punti del .........;
• tutte le coppie del tipo (-; -) individuano punti del .........;
• tutte le coppie del tipo (...; 0) individuano punti del .........;
• tutte le coppie del tipo (...; ...) individuano punti dell’asse y.

ESERCIZIO 21. Sono assegnati i punti A(3;-1), B(3; 5),M(-1;-1), N(-1;-7). È vero che AB = MN?

ESERCIZIO 22. Sono assegnati i punti A(1; 5), B(-4; 5), C(-4;-2), D(5;-2). Quale poligono si ottiene congiungendo nell’ordine i quattro punti assegnati? Determinare l’area del quadrilatero ABCD.

ESERCIZIO 23. Determina l’area del quadrilatero MNPQ sapendo cheM(6;-4), N(8; 3), P(6; 5), Q(4; 3).

ESERCIZIO 24. Determina AB sapendo che A(7;-1) e B(-3;-6).

ESERCIZIO 25. Determina la distanza di P (-3; 2;5) dall’origine del riferimento.

ESERCIZIO 26. Calcola la misura del perimetro del triangolo ABC di vertici A(3;-2), B(4; 1), C(7;-4).

ESERCIZIO 27. Determina il perimetro del quadrilatero di vertici A(1; 5), B(-4; 5), C(-4;-2), D(5;-2).

ESERCIZIO 28. Determina il perimetro del quadrilatero di verticiM(6;-4), N(8; 3), P(6; 5), Q(4; 3).

ESERCIZIO 29. Determina il perimetro e la misura delle diagonali del quadrilatero di vertici A(1;-3), B(4; 3), C(-3; 1), D(-6;-5). ESERCIZIO 30. Verifica che il triangolo di vertici E(4; 3), F(-1; 4), G(3;-2) è isoscele.

ESERCIZIO 31. Il triangolo ABC ha il lato BC appoggiato sull’asse x; il vertice B ha ascissa 5/4, il vertice C segue B e BC = 17/2. Determina le coordinate del vertice C, l’area e il perimetro del triangolo sapendo che il terzo vertice è A(-1; 5).

ESERCIZIO 32. I punti F(3; 0), O(0; 0), C(0; 5) sono i vertici di un rettangolo; determina le coordinate del quarto vertice, il perimetro, l’area e la misura delle diagonali del rettangolo.

ESERCIZIO 33. I punti O(0; 0), A(4; 5), B(9; 5), C(3; 0) sono i vertici di un trapezio. Determina perimetro e area del trapezio OABC.

ESERCIZIO 34. Determina le coordinate del punto medio dei segmenti i cui estremi sono le seguenti coppie di punti:

• A. A(-√2; 0), B(0; √2);
• B. A(2/3; -3/2), B(-1/6; 3);
• C. A(-1; 4), B(1; -4);
• D. A(0; -3/2), B (-2; -1);
• E. A(1 + √2; 1/√3), B(-√2; - √3/3);
• F. A(7/5; -7/5), B(1; -1);
• G. A(-3; 1/2), B(1/2; -3).

ESERCIZIO 35. I vertici del triangolo ABC sono i punti A(2/3; - 3/2), B(- 1/6; 1), C(4/3; 0), determina le coordinate dei puntiM, N, P, punti medi rispettivamente dei lati AB, AC, BC.

ESERCIZIO 36. I vertici del triangolo ABC sono i punti A(-3; 5), B(3;-5), C(3; 5), i puntiM, N, P sono i punti medi rispettivamente dei lati AB, AC, BC. Determina il perimetro di ABC e di MNP. Quale relazione sussiste tra i perimetri ottenuti? Secondo te vale la stessa relazione anche tra le aree dei due triangoli?

ESERCIZIO 37. Verifica che il triangolo di vertici A(2; 3), B(6;-1), C(-4;-3) è rettangolo (è sufficiente verificare che le misure dei lati verificano la relazione di Pitagora). È vero che CB è l’ipotenusa? Verifica che AM, conMpunto medio di BC è metà di BC stesso. Come sono i triangoli AMC e AMB?

ESERCIZIO 38. Verifica che i segmenti AB e CD di estremi A(1/2; 2), B(- 3/4;-2), C(3; 1), D(- 7/2;-1) hanno lo stesso punto medio. È vero che AC = BD?'

Il grafico di una funzione

ESERCIZIO 39. Sono assegnate alcune funzioni con una formula; compila le tabelle a seguito di ciascuna e rappresenta graficamente le funzioni.

ESERCIZIO 40. Esprimi con linguaggio comune la funzione f1 dell’esercizio precedente e rispondi alle domande:

• A. qual è l’immagine di 0? y = ......;
• B. quale elemento del dominio ha per immagine 5? x = ......;
• C. è vero che ogni numero positivo ha l’immagine positiva? Perché?
• D. è vero che -1 è immagine di -2? Perché?

ESERCIZIO 41. Dopo aver determinato per ciascuna delle seguenti funzioni il coefficiente angolare k, tracciane il grafico in un riferimento cartesiano ortogonale:

• A. f₁ : y = 1/2 x;
• B. f₂ : y = x;
• C. f₃ : y = 4/3 x;
• D. f₄ : y = 3/5 x;
• E. f₅ : y = 5x;
• F. f₆ : y = -1/2 x;
• G. f₇ : y = -x;
• H. f₈ : y = -3/4 x.

ESERCIZIO 42. Riporta in uno stesso riferimento cartesiano ortogonale le prime cinque funzioni dell’esercizio precedente. Evidenzia con un colore diverso la funzione f₂, calcola poi il coefficiente angolare k compilando la seguente tabella:

Cancella i termini errati presenti nelle seguenti affermazioni:

• A. Tutte le funzioni hanno coefficiente angolare positivo/negativo;
• B. Tutte le rette formano con l’asse orientato delle x un angolo ottuso/acuto;
• C. Tutte le rette aventi coefficiente minore di 1 stanno sopra/sotto la f₂;
• D. Tutte le rette aventi coefficiente maggiore di 1 stanno sopra/sotto la f₂.

ESERCIZIO 43. Ripeti l’esercizio precedente per le altre tre funzioni (f₆, f₇ e f₈) evidenziando la funzione f₇; costruisci l’analoga tabella e cancella i termini errati presenti nelle seguenti affermazioni:

• A. Tutte le funzioni hanno coefficiente angolare positivo/negativo;
• B. Tutte le rette formano con l’asse orientato delle x un angolo ottuso/acuto;
• C. Tutte le rette aventi coefficiente minore di -1 stanno sopra/sotto la f₇;
• D. Tutte le rette aventi coefficiente maggiore di -1 stanno sopra/sotto la f₇.

ESERCIZIO 44. Se x rappresenta la misura del lato di un triangolo equilatero, determina la misura della sua altezza (al variare della misura del lato). Nel riferimento cartesiano ortogonale traccia il grafico della funzione ottenuta.

ESERCIZIO 45. Quale deve essere la misura del lato di un quadrato per avere la diagonale di 2m?

ESERCIZIO 46. Traccia nel riferimento cartesiano ortogonale il grafico delle funzioni: y = -2, y = 6, y = 0, y = -1, y = 3. ESERCIZIO 47. Traccia nel riferimento cartesiano le funzioni y = 1 e y = -3; nello stesso riferimento traccia la funzione y = 2x. Le tre rette individuano nel piano due punti P e Q. Determina la distanza tra P e Q.

ESERCIZIO 48. Le due funzioni f1 e f2 di proporzionalità diretta assegnate dalle tabelle seguenti delimitano sulla funzione y = -2 un segmento; determina la misura del segmento e il suo punto medio:

'ESERCIZIO 49. Traccia il grafico cartesiano delle funzioni f₁ : y = 2x, f₂ : y = - 1/ 2x, f₃ : y = 2 e indica con A e B rispettivamente i punti di intersezione di f₁ con f₃ e di f₂ con f₃. Considera il triangolo AOB (O è l’origine del riferimento). È vero che AB² = AO² + OB²? Sai trarre una caratteristica del triangolo AOB? Traccia nello stesso riferimento la funzione f4 : y-4 e indica con C e D rispettivamente i punti di intersezione di f1 con f4 e di f2 con f4. Calcola l’area del quadrilatero ABCD.

ESERCIZIO 50. Sono assegnate le funzioni lineari: f₁ : y = 1/2 x - 2, f₂ : y = -x - 3/4, f₃ : y = 6x - 6. Rappresentale in un riferimento cartesiano ortogonale dopo aver compilato per ciascuna una tabella di valori.

Rappresentale in un riferimento cartesiano ortogonale dopo aver compilato per ciascuna una tabella di valori.

ESERCIZIO 51. Segna nel riferimento cartesiano ortogonale i punti assegnati tramite la tabella:

La funzione assegnata è una proporzionalità diretta?

Scrivi la formula y = .........

Completa ora la tabella avente i medesimi valori della variabile indipendente, ma i valori della variabile dipendente siano ottenuti dai precedenti diminuiti di 2:

Scrivi la formula della nuova funzione y = .........

Traccia il suo grafico nello stesso riferimento. È una funzione lineare?

ESERCIZIO 52. La tabella seguente individua coppie di punti allineati; trova la formula che descrive ciascuna funzione lineare e traccia il suo grafico:

ESERCIZIO 53. Traccia il grafico delle seguenti funzioni di proporzionalità inversa:

• A. f1 : y = - 3/2x;
• B. f2 : y = 1/x;
• C. f3 : y = 5/x;
• D. f4 : y = -3/x;
• E. f5 : y = - 1/x;
• F. f6 : y = - 2/5x.

'ESERCIZIO 54. Traccia nelle stesso riferimento cartesiano ortogonale la curva γ : y = - 1/2x e le rette r₁ : y = 2 e r₂ : y = -2. Verifica che l’origine del riferimento è il punto medio del segmento avente per estremi i punti A₁ = r₁ ∏ γ e A₂ = r₂ ∏ γ.

ESERCIZIO 55. Traccia il grafico delle seguenti funzioni di proporzionalità quadratica:

• A. f₁ : y = -x²;
• B. f₂ : y = x²;
• C. f₃ : y = - 1/2 x²;
• D. f₄ : y = - 5/2 x²;
• E. f₅ : y = 3/4 x²;
• F. f₆ : y = 7/3 x².

ESERCIZIO 56. Dai grafici dell’esercizio precedente trai le conclusioni sulla parabola y = k * x², completando

• A. se k > 0 allora i punti della parabola si trovano .........;
• B. se k < 0 allora i punti della parabola si trovano .........;
• C. se k > 1 allora la curva è più aperta o più chiusa rispetto alla y = x²? .........;
• D. se 0 < k < 1 allora la curva è più aperta o più chiusa rispetto alla y = x²? .........;
• E. se k < -1 allora la curva è più aperta o più chiusa rispetto alla y = -x²? .........;
• F. se -1 < k < 0 allora la curva è più aperta o più chiusa rispetto alla y = -x²? ..........

ESERCIZIO 57. Determina la distanza del punto di ascissa x = -2 della parabola y = 3x² dal suo vertice.

ESERCIZIO 58. Sono assegnate le funzioni f₁ : y = (-x)² e f₂ : y = -x² di proporzionalità quadratica. Spiega se e perché sono o non sono la stessa funzione. Danne di ciascuna la descrizione in linguaggio comune. Costruisci per ciascuna una tabella di valori e costruisci il rispettivo grafico. Puoi confermare la risposta data alla prima domanda?

ESERCIZIO 59. Completa la seguente tabella:

Traccia nel riferimento cartesiano ortogonale le funzioni assegnate. Per quali di esse è vero che per qualunque x del dominio è IM. = R?

ESERCIZIO 60. Il rettangolo ABCD ha il lato AB triplo del lato BC. Indica BC = x; determina il perimetro del rettangolo in funzione di x: 2p = ......... Spiega perché è necessaria la condizione x > 0; rappresenta graficamente la funzione perimetro nel riferimento cartesiano. Determina ora l’area in funzione di x: Area = .........; rappresenta la funzione area, nello stesso riferimento.

ESERCIZIO 61. Il triangolo rettangolo ABC, retto in A ha i cateti l’uno doppio dell’altro. Indica la misura del cateto minore AB = x e spiega perché è necessaria la condizione x > 0. Determina l’area del triangolo in funzione di x: Area = .........; rappresenta questa funzione nel riferimento cartesiano ortogonale. Stabilisci le misure dei cateti se l’area è di 20 cm². Calcola il perimetro del triangolo in funzione di x: 2p = .........; rappresenta come varia la funzione perimetro al variare di x nel riferimento cartesiano ortogonale.

ESERCIZIO 62. Nel triangolo isoscele ABC il lato obliquo AB è doppio della base BC; indica BC = x e determina in funzione di x il perimetro del triangolo. 2p = ......... Di che funzione si tratta? Descrivila e rappresentala nel riferimento cartesiano ortogonale, dopo aver fissato le opportune condizioni sulla variabile indipendente. Se il perimetro è 120 cm, quanto misurano i lati del triangolo? Calcola, in questo caso, l’area del triangolo e la misura delle altezze relative ai lati uguali.

ESERCIZIO 63. Traccia il grafico delle seguenti funzioni.

ESERCIZIO 64. Traccia il grafico della funzione y = |x + 1|.

ESERCIZIO 65. Un caseificio vende mozzarelle a € 4,50 al chilo ai clienti che ne acquistano fino 10 kg; per i clienti che fanno acquisti superiori ai 10 kg vende a € 4,00 al kg per la parte che eccede i 10 kg e per i primi 10 kg vende sempre a e 4,50/kg. Per i clienti dei grandi supermercati che acquistano quantità superiori a 100 kg vende a € 3,50 al kg. Codifica con opportune formule la funzione costo:

Determina il costo dei seguenti ordini:

Rappresenta graficamente la funzione nel riferimento cartesiano ortogonale.

ESERCIZIO 66. Dai grafici delle funzioni di seguito riportati, per ognuna di esse stabilisci insieme di definizione D, insieme immagine IM. e verifica se la funzione è iniettiva, suriettiva o biettiva.