Esercizi sulle frazioni e i numeri razionali (superiori)
I seguenti esercizi riguardano le frazioni e i numeri razionali studiati nella Lezione 3. Essi sono divisi per paragrafi in modo tale da favorire la scelta degli esercizi specifici.
Frazione
[modifica]ESERCIZIO 1. Da un cartoncino rettangolare quadrettato di lati rispettivamente 5 unità e 8 unità viene ritagliata la forma colorata in grigio, come mostrato nella figura di seguito riportata.

Quale frazione rappresenta il rapporto tra la forma ritagliata e il cartoncino?
ESERCIZIO 2. Il monte-premi di una lotteria è di € 50000. Il primo premio è di € 25000, il secondo di € 10000, il terzo di € 5000, il quarto di € 4000, il quinto e il sesto premio sono uguali. Nella figura un quadretto rappresenta € 1000 ed il totale è il monte-premi.

- A. Colora con colori diversi i quadretti che servono per rappresentare i sei premi, un colore per ogni premio.
- B. Quale parte del monte-premi è stata incassata da chi ha vinto il secondo premio? Esprimi questa parte con una frazione.
- C. Marco ha vinto il sesto premio: quanto ha vinto?
ESERCIZIO 3. La figura seguente è composta da 11 quadratini, alcuni bianchi altri grigi.

Quale frazione rappresenta la parte grigia rispetto all'intera figura? Quale frazione la parte bianca?
ESERCIZIO 4. Di ciascuna figura colora la parte indicata dalla frazione.
ESERCIZIO 5. Indica se le frazioni sono proprie (P), improprie (I) o apparenti (A).
- A. 3/4 P I A.
- B. 8/3 P I A.
- C. 12/3 P I A.
- D. 5/2 P I A.
- E. 5/3 P I A.
- F. 3/2 P I A.
ESERCIZIO 6. Trova le frazioni equivalenti completando.
- A. 3/4 = .../12.
- B. 12/16 = 3/....
- C. 5/2 = .../10.
- D. 21/35 = .../5.
ESERCIZIO 7. Sottolinea le frazioni equivalenti a 3/5 tra le seguenti.
- 6/10.
- 25/100.
- 12/10.
- 5/25.
ESERCIZIO 8. Completa le seguenti uguaglianze.
- A. 3/5 = .../10.
- B. 75/10 = .../100.
- C. 7/... = 1/2.
- D. 3 = 24/....
ESERCIZIO 9. Indica almeno tre frazioni equivalenti a ciascuna delle seguenti.
- A. 5/6.
- B. 3/5.
- C. 12/60.
- D. 2/3.
- E. 1/2.
- F. 5/2.
ESERCIZIO 10. Nella figura che segue il quadratino colorato rappresenta 1/4 del quadrato grande; costruisci una figura che rappresenti 8/4 del quadrato grande accostando opportunamente altri quadrati uguali.

ESERCIZIO 11. Riduci ai minimi termini le seguenti frazioni.
- A. 4/6.
- B. 8/2.
- C. 2/10.
- D. 18/16.
- E. 3/12.
- F. 6/20.
- G. 80/100.
- H. 8/12.
- I. 9/6.
- J. 10/15.
- K. 14/49.
- L. 15/21.
ESERCIZIO 12. Riduci ai minimi termini le seguenti frazioni.
- A. 16/6.
- B. 18/15.
- C. 20/12.
- D. 21/9.
- E. 24/30.
- F. 25/15.
- G. 27/21.
- H. 28/14.
- I. 30/16.
- J. 32/24.
- K. 35/10.
- L. 36/81.
- M. 40/6.
- N. 42/21.
- O. 45/27.
- P. 48/60.
- Q. 12/30.
- R. 135/77.
ESERCIZIO 13. Si può dire che la parte colorata in grigio della Figura 4 corrisponde a 1/5 della figura stessa?

ESERCIZIO 14. Costruisci una figura che corrisponde a 11/6 della Figura 5.
ESERCIZIO 15. Per quali dei seguenti disegni la parte colorata in grigio rappresenta sempre la frazione 3/4 del quadrato bianco?

ESERCIZIO 16. Relativamente alla Figura 6, quale proposizione è vera?
- A. Il segmento AB la divide in due parti uguali.
- B. Il segmento AB la divide in due quadrilateri.
ESERCIZIO 17. La parte in grigio rappresenta 1/4 della Figura 7?
ESERCIZIO 18. Costruisci una figura che sia gli 11/6 della Figura 8.
ESERCIZIO 19. Colora i 3/4 della Figura 9.
ESERCIZIO 20. Il segmento nel disegno rappresenta i 3/5 dell'intero.

Ti basta questa informazione per costruire l'intero? Come procederesti?
ESERCIZIO 21. Disegna un segmento come grandezza unitaria e dimostra che la frazione 3/5 è equivalente a 6/10 ma non a 9/25.
Dalle frazioni ai numeri razionali
[modifica]ESERCIZIO 22. Riscrivi le seguenti frazioni improprie come somma di un numero naturale e una frazione propria.
- 10/3.
- 17/9.
- 11/2.
- 25/3.
- 17/10.
- 15/6.
La scrittura dei numeri razionali
[modifica]ESERCIZIO 23. Senza eseguire le divisioni indica quali di queste frazioni possono essere scritte come numero decimale finito (DF), quali come numero decimale periodico (DP) e quali come numero intero (I):
- A. - 3/2 DF DP I.
- B. - 6/5 DF DP I.
- C. 2/25 DF DP I.
- D. 5/8 DF DP I.
- E. 5/6 DF DP I.
- F. - 5/12 DF DP I.
- G. 12/6 DF DP I.
- H. 5/10 DF DP I.
ESERCIZIO 24. Trasforma le seguenti frazioni in numeri decimali.
- A. 13/2.
- B. 11/3.
- C. 3/5.
- D. 15/6.
- E. 17/7.
- F. 15/8.
- G. 12/9.
- H. 127/10.
- I. 122/11.
- J. 13/12.
- K. 35/121.
- L. 121/35.
- M. 12/10.
- N. 127/100.
- O. 122/1100.
- P. 13/100.
- Q. 35/1000.
- R. 121/10000.
- S. 12/5.
- T. 13/7.
- U. 15/4.
- V. 5/8.
- W. 32/9.
- X. 21/20.
- Y. 37/18.
ESERCIZIO 25. Trasforma le seguenti frazioni in numeri decimali.
- A. 4/12.
- B. 20/15.
- C. 135/1.
- D. 28/49.
- E. 45/9.
- F. 8/50.
- G. 36/1080.
- H. 55/6875.
- I. 54/648.
- J. 25/0,0000002.
- K. 40/0,000002.
- L. 45/0,00009.
- M. 0,008/10X10−3.
- N. 800/5X104.
- O. 8X102/50000.
- P. 124/33X26.
- Q. 8X10−3/0,005.
- R. 23X1000/500.
- S. 28X58/108.
- T. 318/99.
ESERCIZIO 26. Trasforma in frazioni i seguenti numeri decimali.
- A. 12,5.
- B. 4,2.
- C. 6,25.
- D. 3,75.
- E. 0,1.
- F. 2,5.
- G. 100,100.
- H. 0,12.
- I. 1,1030.
- J. 0,00100.
- K. 100,0010.
- L. 0,0001.
- M. 1,25.
- N. 0,08.
- O. 1,002.
- P. 15,675.
- Q. 1,7.
- R. 1,46.
- S. 0,13.
- T. 0,149.
- U. 5,015.
- V. 3,21.
- W. 2,3.
- X. 1,086.
ESERCIZIO 27. Completa la tabella.
| NUMERO DECIMALE | PARTE INTERA | PARTE DECIMALE | PERIODO | ANTIPERIODO | FRAZIONE |
|---|---|---|---|---|---|
| 1,7521 | |||||
| 3,75 | |||||
| 12,124 | |||||
| 1,05 | |||||
| 0,1357 |
ESERCIZIO 28. Trasforma i seguenti numeri decimali in frazioni.
- A. -1,25.
- B. 0,03.
- C. -2,1.
- D. 0,13.
- E. 5,080.
- F. 3,752.
- G. -0,38.
- H. 11,175.
- I. 0,0102.
- J. 0,12345.
- K. 100,100.
- L. 100,001.
- M. 0,08.
- N. 0,2.
- O. 0,1.
- P. 0,03.
- Q. 23,5.
- R. 22,32.
- S. 0,25.
- T. 31,02.
- U. 0,21.
- V. 2,34.
- W. 3,218.
- X. 0,034.
ESERCIZIO 29. Scrivi delle frazioni equivalenti ai seguenti numeri decimali.
- A. 0,00355.
- B. 3,7.
- C. 7,84.
- D. 0,004X105.
- E. 0,0013.
- F. 7,42.
- G. -0,006.
- H. 3X10−4.
ESERCIZIO 30. Scrivi la frazione generatrice di 12;345. Qual è la 614-esima cifra decimale del numero?
ESERCIZIO 31. Calcola 0,9 - 3,9. Cosa osservi?
ESERCIZIO 32. Verifica le seguenti uguaglianze trovando la frazione generatrice.
- 1,7/1,3 = 1,3.
- 2,7/1,6 = 1,6.
- 1,16/2,3 = 0,5.
- 2,3/1,6 = 1,4.
I numeri razionali e la retta
[modifica]ESERCIZIO 33. Rappresenta su una retta orientata, dopo aver scelto una opportuna unità di misura, i seguenti gruppi di numeri razionali, ciascun gruppo su una retta.
- A. 3/4, 3/8, 1/3, 5/4, 2/5, 6/3, 5/6, 12/4, 19/8, 16/5.
- B. 2/3, - 3/4, 5/2, - 7/12, 3/2, - 11/6, 9/4.
- C. 0/4, 5/4, 9/4, 1/2, 19/8, 3/2, 7/4, 4/2.
- D. 10/3, 5/3, 2, 0/3, 4/3, 2/3, 5/6, 13/6.
- E. 1/2, 3/4, - 5/4, - 1/2, 7/8, - 5/16.
- F. 8/5, 1/2, 3/10, - 7/4, - 3/5, - 11/10.
ESERCIZIO 34. Scrivi i numeri razionali rappresentati dai punti segnati sulla retta nella figura.

A = ..., B = ..., C = ..., D = ..., E = ..., F = ....
ESERCIZIO 35. Disegna su una retta orientata i seguenti numeri decimali, ciascun gruppo su una retta diversa.
- A. 0,6, 2,3, -1,2, -0,06, 0,3, 0,9.
- B. 1,4, -0,3, -1,5, 0,2, -0,9, 0,15.
- C. -0,8, -1,6, +4,91, -1,17, 3,5, -2,8.
- D. 1,55, 2,01, -3,0, -2,10, 0,25, -0,75.
Confronto tra numeri razionali
[modifica]ESERCIZIO 36. Inserisci tra le seguenti coppie di numeri razionali i simboli di maggiore (>), minore (<) o uguale (=).
- A. 4/5 ... 5/7.
- B. - 9/5 ... - 8/3.
- C. -1 ... 1/12.
- D. 2/7 ... 6/21.
- E. - 1/2 ... - 3/4.
- F. 3/5 ... 6/9.
ESERCIZIO 37. Riscrivi in ordine crescente (dalla più piccola alla più grande) le seguenti frazioni.
- A. 2/3, 3/4, 5/8, 3/5, 7/12.
- B. - 2/3, - 3/4, - 5/6, - 1/2, - 2/5.
- C. - 2/3, 3/4, - 5/6, 1/2, - 1, - 2/5, 0.
- D. - 3/2, 4/3, - 6/5, 2/5, - 1, 5/2, 0.
- E. 3/4, 4/3, 11/12, 5/3, 2/3, 2/7, 3/2.
ESERCIZIO 38. Ordina dal più piccolo al più grande i seguenti valori.
- A. 10,011, 10,110, 11,001, 11,100.
- B. 10,01, 11,11, 10,101, 10,001.
- C. 0,101, 0,011, 0,110, 0,0101.
- D. 1,0101, 1,1001, 1,0011, 1,0110.
ESERCIZIO 39. Scrivi una frazione molto vicina a - 2/9.
ESERCIZIO 40. Scrivi una frazione compresa tra:
- A. 3/5 e 7/10.
- B. 5/3 e 1/7.
- C. 1/2 e 2/3.
ESERCIZIO 41. Quali disuguaglianze sono vere?
- A. - 7/6 < - 6/7. V F.
- B. - 7/6 > + 6/7. V F.
- C. - 7/6 < + 6/7. V F.
- D. + 7/6 < - 6/7. V F.
- E. + 7/6 < + 6/7. V F.
- F. + 7/6 > - 6/7. V F.
ESERCIZIO 42. Quale dei seguenti numeri è più vicino a 1?
- A. 0,10.
- B. 0,99.
- C. 0,01.
- D. 0,90.
ESERCIZIO 43. Quale dei seguenti numeri è più vicino alla frazione 1/10 ?
- A. 0,01.
- B. 0,90.
- C. 1,01.
- D. 0,19.
ESERCIZIO 44. Scrivi due numeri compresi tra:
- A. 2,3 e 3,4.
- B. 3,4 e 3,6.
- C. 2,3 e 2,4.
- D. 1,13 e 1,23.
- E. 3,4 e 3,6.
- F. 1,35 e 1,36.
Le operazioni con i numeri razionali
[modifica]ESERCIZIO 45. Calcola le seguenti somme algebriche tra frazioni.
- A. 1/2 + 3/2.
- B. 7/11 + 4/11.
- C. 3/2 - 5/2.
- D. 8/18 + 5/9.
- E. 6/5 + 0.
- F. - 3/2 + 4/3.
- G. - 2/3 + 3/4.
- H. 4/3 - 6/5.
- I. 2/5 + 5/8.
- J. 5/8 + 5/6.
- K. 5/6 - 5/12.
- L. 1 - 3/2.
- M. 11/5 + 5.
- N. 7/3 - 6/4.
- O. 3 - 2/3.
- P. 1/5 - 1.
- Q. 4 + 3/2 - 3/4.
- R. 4/3 + 3 - 1/2.
- S. 3/4 + 1/4 - 5/4.
- T. 1 - 1/2 + 1/3 - 1/4.
ESERCIZIO 46. Calcola le seguenti somme algebriche fra numeri razionali.
- A. 1,6 + 2/3.
- B. 5,1 - 1,5.
- C. 0,03 + 0/3.
- D. 0,16 - 1;45.
- E. 50% + 1/2.
- F. 2/5 - 1,2 + 5%.
- G. -1,2 + 25% + 5/18.
- H. 3/2 - 13% + 0,15.
- I. 1,2 + 1,2 + 1/2 + 1,2%.
- J. 7,9892 + 3,1218.
- K. 3,999 + un centesimo.
ESERCIZIO 47. Completa:
- 3/4 + ... = 1.
- 1 - ... = 4/13.
- 11/12 * ... = 8/55.
- ... : 5/3 = 3/5
ESERCIZIO 48. Completa la seguente tabella.
| a | - 2/3 | + 3/4 | -1 | 0 | - 1,6 | - 5 | - 0,21 |
|---|---|---|---|---|---|---|---|
| B | + 7/3 | - 5/8 | + 2/5 | 15% | +2,3 | + 17/3 | + 3/5 |
| A+b | |||||||
| A-b | |||||||
| B-a | |||||||
| -A-b | |||||||
| -A+b |
ESERCIZIO 49. Completa la seguente tabella.

ESERCIZIO 50. Calcola a mente:
- A. 0,1 + 0,1.
- B. 0,2 + 0,8.
- C. 0,01 + 0,9.
- D. 0,91 + 0,19.
- E. 1,10 + 1,01.
- F. 0,999 + 0,10.
- G. 1,1 - 0,9.
- H. 100 - 0,99.
- I. 2 - 0,1.
- J. 3 - 1,1.
- K. 4 - 1,4.
- L. 10 - 0,10.
ESERCIZIO 51. Calcola i seguenti prodotti fra frazioni.
- A. 3/2 * 4/3.
- B. 6 * 5/2.
- C. - 6/5 * (- 4/3).
- D. 2/3 * 2/9.
- E. 5/5 * 5/8 * (- 5/6).
- F. 3/2 * (- 8/9) * 5/6.
ESERCIZIO 52. Calcola i seguenti prodotti fra numeri razionali.
- -1,1 * 18/5.
- 2% * 5%.
- - 3/4 * (-120%).
ESERCIZIO 53. Completa la seguente tabella.
| a | - 2/3 | + 3/4 | - 5/8 | 15% | - 1,6 | + 17/3 | - 0,21 |
|---|---|---|---|---|---|---|---|
| B | + 7/3 | - 5/2 | +2,3 | + 5/3 | |||
| A*b | 1 | -1 | 0 |
ESERCIZIO 54. Completa la seguente tabella.

ESERCIZIO 55. Calcola a mente:
- A. 0,1 * 0,1.
- B. 1/10 * 1/10.
- C. 0,1 * 100.
- D. 1 * 0,1.
- E. 2 * 0,1.
- F. 20 * 0,02.
- G. 0,01 * 10.
- H. 1/100 * 10.
- I. 0,1 * 0,2.
- J. 3/10 * 30.
- K. 0,01 * 0,1.
- L. 1000 * 0,0001.
ESERCIZIO 56. Calcola i seguenti quozienti fra frazioni.
- A. 3/2 : 4/3.
- B. - 6/5 : (- 2/3).
- C. + 3/2 : (- 3/2).
- D. 2/5 : 5/8 : (- 5/6).
ESERCIZIO 57. Calcola i seguenti quozienti fra numeri razionali.
- A. -1,1 : 18/5.
- B. 2% : 5%,
- C. 1/2 : 0,5.
- D. - 3/4 : 1,4 : (-120%).
ESERCIZIO 58. Completa la seguente tabella.
| a | - 2/3 | + 3/4 | -1 | 0 | -1,6 | -5 | -0,21 |
|---|---|---|---|---|---|---|---|
| B | + 7/3 | - 5/8 | + 2/5 | 15% | +2,3 | + 17/3 | + 3/5 |
| A:b | |||||||
| B:a |
ESERCIZIO 59. Calcola a mente:
- A. 0,30 * 0,40.
- B. 0,5 : 0,1.
- C. 0,5 * 0,2.
- D. 0,1 * 0,1.
- E. 0,4 * 3.
- F. 0,1 : 0,1.
- G. 0,5 * 20.
- H. 0,1 * 0,010.
ESERCIZIO 60. Esegui le seguenti operazioni con le frazioni, quando è possibile.
- A. 2/3 * 0.
- B. 1/2 - 1/2.
- C. 1/2 * 2/0.
- D. 1/2 * 0/2.
- E. 1/2 * 1/2.
- F. 2/3 : 0.
- G. 2/3 - 0.
- H. 1 : 2/3.
- I. 1/4 * 4.
- J. 1/4 : 4.
- K. 0,3 : 3.
- L. 1,5 : 1,5.
- M. 1,5 : 1,5.
- N. 1,50.
- O. (1 - 1)0.
- P. (-1)−1.
- Q. 30 : 20.
- R. (-2)−2 : (-1)−1.
Potenza di una frazione
[modifica]ESERCIZIO 61. Calcola il valore delle seguenti potenze.
- A. (- 2/3)2.
- B. (- 1/2)3.
- C. (- 3/2)2.
- D. (1/2 - 1)3.
- E. (- 3/5)0.
- F. (- 3/5)1.
- G. -24.
- H. (-2)4.
- I. (- 2/3)−2.
- J. (- 1/2)−3.
- K. - (3/2)−2.
- L. -2−4.
- M. (-2)−4.
- N. - (5/6)−1.
ESERCIZIO 62. Indica quali proprietà delle potenze sono state applicate nelle seguenti uguaglianze.
- A. (- 3/2)2 * (- 3/2)3 = (- 3/2)5 = - 35/25; proprietà . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- B. (- 3/2)2 : (- 3/2)3 = (- 3/2)−1 = - 2/3; proprietà . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- C. ((- 3/2)2)3 = (- 3/2)6 = + 36/26; proprietà . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- D. (5/2)2 : (25/10)2 = (5/2 : 5/2)2 = (5/2 * 2/5)2 = 12; proprietà . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- E. (- 5/2)2 * (6/25)2 = (- 5/2 * 6/25)2 = (- 3/5)2 = + 32/52; proprietà . . . . . . . . . . . . . . . . . . . . .
ESERCIZIO 63. Completa la seguente tabella.
| a | a2 | a−2 | -a2 | (-a)3 | a−1 | a0 | a3 |
|---|---|---|---|---|---|---|---|
| - 2/3 | |||||||
| -1,6 | |||||||
| -0,1 | |||||||
| 3/10 |
ESERCIZIO 64. Calcola a mente.
- A. 3,4 * 102.
- B. 3,4 : 102.
- C. 0,34 * 104.
- D. 34,4 : 102.
- E. 0,34 * 103.
- F. 34,10 * 103.
- G. 3,04 * 10.
- H. 0,34 : 102.
ESERCIZIO 65. Calcola le seguenti potenze prestando particolare attenzione ai segni.
- A. -(-2)2;
- B. [-(-1)2]3.
- C. -(-2)−4;
- D. -[-(-1)−1]−2.
- E. .
- F. .
- G. (-3)3 * .
Notazione scientifica e ordine di grandezza
[modifica]ESERCIZIO 66. Esprimere in notazione scientifica i seguenti numeri.
- A. 780000000000000 = 7,8 * 10....
- B. 423000000000 = 4,23 * 10....
- C. 76000000000000 = ... * 10....
- D. 0,00000000098 = 9,8 * 10....
- E. 0,0000045 = 4,5 * 10....
- F. 0,000000987 = ... * 10....
ESERCIZIO 67. Quale tra i seguenti numeri non è scritto in notazione scientifica?
- A. 5,67 * 10−12.
- B. 4,28 * 108.
- C. 10,3 * 10−2.
- D. 9,8 * 107.
ESERCIZIO 68. Determina in notazione scientifica l'area di una lamina di ferro quadrata avente il lato di misura 0,00000000021 m.
ESERCIZIO 69. Scrivi in notazione scientifica i seguenti numeri.
- 34000.
- 0,000054.
- 26.
- 0,54000.
- 5.
- 0,00001.
- 990000.
- 222.
ESERCIZIO 70. Trasforma i numeri in notazione scientifica e scrivi nella stessa forma il risultato.
- A. 0,00036 * 20000000 = ....
- B. 8400 : 42 = ....
- C. 900000000 : 0,0003 = ....
- D. 3 : 10000000 = ....
ESERCIZIO 71. Calcola ed esprimi il risultato in notazione scientifica.
- A. 3 * 1024 + 4 * 1024.
- B. 0,3 * 10104 + 4 * 10103.
- C. 6 * 10101 * 0,15 * 10101.
- D. 12 * 102000 : 6 * 10200.
ESERCIZIO 72. Trasforma i numeri in notazione scientifica e scrivi nella stessa forma il risultato.
- A. .
- B. .
- C. .
- D. .
- E. .
- F. .
ESERCIZIO 73. Disponi in ordine di distanza dal Sole i seguenti pianeti, in base alla distanza media in km riportata tra parentesi: Mercurio (5,8 * 107), Nettuno (4,5 * 109), Giove (7,8 * 108), Plutone (6,1 * 109), Urano (2,7 * 109), Terra (1,5 * 108), Marte (2,3 * 108).
ESERCIZIO 74. Determina l'ordine di grandezza dei seguenti numeri.
- A. 126000000.
- B. 0,0000098.
- C. 7000000.
- D. 0,0000000027.
ESERCIZIO 75. Completa la seguente tabella.
| Numero | 26000000 | 0,000083 | 490000 | 0,0000081 |
|---|---|---|---|---|
| Notazione scientifica o.d.g. |
ESERCIZIO 76. Determina l'ordine di grandezza del risultato dei seguenti calcoli.
- A. 5,3 * 105 * 1,2 * 103 - 2,5 * 106.
- B. (5 * 102 * 4 * 103)3.
Problemi con le frazioni
[modifica]ESERCIZIO 77. La distanza Roma - Bari è di 450 km. Se ho percorso i 2/5 del tragitto quanti chilometri mancano ancora da percorrere?
ESERCIZIO 78. Lucia ha letto 3/5 di un libro e le rimangono da leggere 120 pagine. Di quante pagine è composto il libro?
ESERCIZIO 79. Una persona possiede e 525. Se spende i 3/5 della somma e poi i 2/3 della rimanente, quale somma di denaro le rimane?
ESERCIZIO 80. Luigi ha 18 anni, cioè i 3/7 dell'età di sua madre, che a sua volta ha i 4/5 dell'età del padre. Quali sono le età del padre e della madre di Luigi?
Le percentuali
[modifica]ESERCIZIO 81. Trasforma i seguenti numeri percentuali in numeri decimali.
- 12%.
- 0,03%.
- 4,3%.
- 80%.
- 3,5%.
- -0,2%.
- 15%.
- -0,38%.
ESERCIZIO 82. Trasforma i seguenti numeri decimali in percentuali.
- -1,25.
- 0,03.
- -2,1.
- 0,13.
- 5,080.
- 3,752.
- -0,38.
ESERCIZIO 83. Trasforma i seguenti numeri percentuali in frazioni ridotte ai minimi termini.
- 12%.
- 0,03%.
- 4,3%.
- 80%.
- 3,5%.
- -0,2%.
- 15%.
- -0,38%.
ESERCIZIO 84. Trasforma le seguenti frazioni in numeri percentuali.
- - 3/2.
- 4/3.
- - 6/5.
- 2/25.
- 5/8.
- 5/6.
- - 5/12.
ESERCIZIO 85. A una scuola di ballo si sono iscritte 120 persone delle quali il 20% frequenta i corsi di ballo liscio. In quanti frequentano i corsi di liscio?
ESERCIZIO 86. Una scuola attiva dei corsi di lingue. 32 studenti si iscrivono al corso di inglese, 24 al corso di francese e 16 al corso di tedesco. Qual è la percentuale degli alunni iscritti al corso di inglese, rispetto al totale degli iscritti?
ESERCIZIO 87. A una scuola di ballo sono iscritte 120 persone e di queste il 68% sono donne. Quanti sono gli uomini?
ESERCIZIO 88. Il prezzo di listino di una bici è di e 175. Se viene venduta con uno sconto del 10% quanto viene a costare?
ESERCIZIO 89. Una canna da pesca da e 125 è in vendita promozionale a e 70. Qual è la percentuale di sconto applicata?
ESERCIZIO 90. Per l'acquisto di un armadio, Maria è riuscita a spuntare, dopo lunghe discussioni con il venditore, uno sconto del 25%, risparmiando ben e 120. Qual era il prezzo dell'armadio prima dello sconto?
ESERCIZIO 91. Completa la seguente tabella.
| Prezzo di listino (€) | Sconto (€) | Sconto (%) | Prezzo scontato (€) |
|---|---|---|---|
| 120 | 12 | 10 | 108 |
| 250 | 10 | ||
| 125 | 5 | ||
| 170 | 10 | ||
| 1100 | 15 | ||
| 220 | 20 | ||
| 12000 | 700 | ||
| 15 | 15 | ||
| 30 | 50 | ||
| 25 | 140 | ||
| 120 | 30 |
ESERCIZIO 92. Calcola:
- A. Il 10% di 100.
- B. Il 30% di 700.
- C. Il 20% di 500.
- D. Il 15% di 150.
- E. Il 25% di 1250.
- F. Il 16% di 120.
ESERCIZIO 93. Quale percentuale è:
- A. 10 bocciati su 120 alunni: la percentuale di bocciati è circa 8,3%.
- B. 15 alunni su 45 giocano a calcio: la percentuale di alunni che giocano a calcio è . . . . . . .
- C. 10 alunni su 28 suonano il piano: la percentuale di alunni che suonano il piano è . . . . . . .
- D. 20 alunni su 120 frequentano il corso di teatro: la percentuale di alunni che fanno teatro è . . . . . .
ESERCIZIO 94. Se il prezzo aumenta:
- A. Un chilo di pane lo scorso anno costava € 1,20 e quest'anno è aumentato del 3%, allora costa . . . . . . .
- B. Un litro di benzina lo scorso anno costava € 1,514, mentre quest'anno costa € 1,629, quindi è aumentata del . . . . . . %.
- C. Un litro di latte lo scorso anno costava € 1,25 e quest'anno è aumentato di 0,05%, quindi costa € . . . . . . .
- D. Un chilo di formaggio parmigiano lo scorso anno costava € 23,50 e quest'anno costa € 25,80 pertanto è aumentato del . . . . . . %.
ESERCIZIO 95. Se il prezzo diminuisce:
- A. Un chilo di pomodori lo scorso anno costava € 1,20 e quest'anno è diminuito del 5%, allora costa € . . . . . . .
- B. Un chilo di peperoni lo scorso anno costava € 2,10, mentre quest'anno costa € 1,80 quindi è diminuito del . . . . . . %.
- C. Un chilo di cicoria lo scorso anno costava € 0,80 e quest'anno due chili costano € 1,20, pertanto la cicoria è diminuita del . . . . . . %.
- D. Un chilo di arance lo scorso anno costava € 1,40, quest'anno le arance sono diminuite del 15%, quindi al chilo costano € . . . . . .
ESERCIZIO 96. Dato il costo di un oggetto IVA esclusa, calcola il prezzo IVA inclusa.
| Costo IVA esclusa (€) | IVA (%) | Costo IVA inclusa (€) |
|---|---|---|
| 130 | 22 | |
| 1250 | 22 | |
| 17,40 | 4 | |
| 10 | 170 | |
| 22 | 12240 | |
| 101,00 | 105,60 |
ESERCIZIO 97. Dati imponibile (costo senza IVA) e IVA, determina il costo comprensivo di IVA e viceversa.
| Imponibile (€) | IVA (%) | IVA (€) | Totale |
|---|---|---|---|
| 100 | 21 | 21 | 121 |
| 1100 | 21 | ||
| 1 | 23 | 1100 | |
| 1000 | 1100 | ||
| 21 | 141 | ||
| 1100 | 100 |
ESERCIZIO 98. La seguente tabella riporta i dati relativi alla provenienza degli alunni di una prima classe di una scuola secondaria.
Scuole di provenienza
| Sesso | Scuola A | Scuola B | Scuola C | Altre Scuole |
|---|---|---|---|---|
| M | 6 | 4 | 4 | 2 |
| F | 5 | 3 | 4 | 2 |
- A. Qual è la percentuale di alunni provenienti dalla Scuola A?
- B. Qual è la percentuale di maschi provenienti dalla Scuola C?
- C. Qual è la percentuale di alunni che non provengono dalle scuole A o B o C?
- D. Qual è la percentuale di alunni che provengono dalle scuola A o C?
ESERCIZIO 99. Agli esami di stato, un gruppo di allievi (A) ha riportato i seguenti punteggi (P) in centesimi.
| P | 60 | 68 | 70 | 74 | 75 | 80 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 94 | 98 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 2 | 1 | 3 | 4 | 2 | 3 | 2 | 3 | 4 | 1 | 3 | 2 | 1 | 3 | 4 | 6 | 8 |
Per poter partecipare a un concorso occorre aver conseguito il diploma con un punteggio superiore a 75. Quale percentuale di diplomati potrà partecipare al concorso? Se solo il 10% di quelli che si sono presentati al concorso lo hanno superato, quanti degli allievi hanno superato il concorso?
ESERCIZIO 100. Tra i dipendenti di un'azienda si effettua un sondaggio per decidere se è opportuno introdurre un nuovo tipo di turno di lavoro. Nella tabella sono riportati i risultati del sondaggio.
| Lavoratori | Favorevoli | Contrari |
|---|---|---|
| Uomini | 75 | 49 |
| Donne | 81 | 16 |
- A. Tra le donne, qual è la percentuale di lavoratrici favorevoli al nuovo turno?
- B. Qual è la percentuale di lavoratori (uomini e donne) che non sono favorevoli al nuovo turno?
ESERCIZIO 101. Sapendo che AB = 12 cm e che BC = 3/4 AB, calcola la lunghezza di BC.
ESERCIZIO 102. Sapendo che AB = 36 cm e che AB = 6/5 BC, calcola la lunghezza di BC.
ESERCIZIO 103. Sapendo che AB + BC = 15 cm e che AB = 23 BC, calcola le lunghezze di AB e BC.
ESERCIZIO 104. Sapendo che AB - BC = 4 cm e che AB = 43 BC, calcola le lunghezze di AB e BC.
ESERCIZIO 105. Determina le ampiezze di due angoli complementari sapendo che uno è la metà dell'altro.
ESERCIZIO 106. Determina le ampiezze di due angoli supplementari sapendo che uno è i 2/3 dell'altro.
ESERCIZIO 107. Determina le misure dei due lati di un rettangolo sapendo che ha perimetro di 128 cm e che l'altezza è 3/2 della base.
ESERCIZIO 108. La superficie della Toscana è divisa tra le seguenti provincie delle quali è fornita tra parentesi l'estensione in km2, calcola per ciascuna di esse la percentuale del territorio posseduta: Arezzo (3235), Firenze (3514), Grosseto (4504), Livorno (1211), Lucca (1773), Massa e Carrara (1156), Pisa (2444), Pistoia (965), Prato (365), Siena (3821).
ESERCIZIO 109. La superficie della Terra è per il 70% ricoperta di acqua e per il 30% di terraferma. Per 1/5 la terraferma è coperta da ghiaccio e deserto, per 2/3 da foreste e montagna. La parte rimanente è terreno coltivato. Qual è in percentuale la parte della superficie terrestre coltivata?
ESERCIZIO 110. In 30 kg di sapone concentrato al 30% quanta acqua e quanto sapone ci sono?
ESERCIZIO 111. Una succo di frutta di 6 kg contiene il 45% di frutta. Quanta frutta devo aggiungere per avere una nuova soluzione di succo di frutta al 60%.
ESERCIZIO 112. Quanta acqua bisogna aggiungere a una soluzione di 2 kg concentrata al 12% per ottenere una nuova soluzione concentrata al 10%?
ESERCIZIO 113. Si hanno due soluzioni delle stesse sostanze, una concentrata al 10% e l'altra al 30%. In quale proporzione occorre miscelare le due soluzioni in modo da ottenere 6 kg di soluzione concentrata al 15%?
ESERCIZIO 114. Una società ha acquistato dei PC nuovi per i propri dipendenti. Pagandoli in contanti ha ottenuto uno sconto dell'8%, versando di conseguenza l'importo di € 24500. Qual era il valore iniziale della merce acquistata?'
ESERCIZIO 115. Una persona paga un tappeto € 1200, lo stesso tappeto l'anno precedente costava € 900. Quanto è stato l'aumento percentuale da un anno all'altro?
ESERCIZIO 116. Quanto vale il 2012% di 2012?
Proporzioni
[modifica]ESERCIZIO 117. Verifica quale delle seguenti scritture formano una proporzione.
- A. 10 : 11 = 12 : 13.
- B. 7 : 14 = 21 : 42.
- C. 64 : 48 = 8 : 6.
- D. 18 : 15 = 12 : 10.
- E. 10 : 6 = 5 : 3.
- F. 1,2 : 1,4 = 3,6 : 4,2.
ESERCIZIO 118. Disponi opportunamente i numeri in modo che formino una proporzione.
- A. 7 5 20 28.
- B. 8 3 2 12.
- C. 5 6 2 15.
- D. 3 5 9 15.
- E. 6 7 2 21.
- F. 3 8 6 16.
ESERCIZIO 119. Completa la seguente tabella.
| 1° termine | 2° termine | Antecedente | Conseguente | Rapporto | Rapp. inverso |
|---|---|---|---|---|---|
| 38 | 8 | 32 | 8 | 32 : 8 = 4 | 8/32 = 1/4 |
| 12 | 13 | ||||
| 3/5 | 3 | ||||
| 1/4 : 3/2 = 1/6 | |||||
| 7/10 = 21/30 |
ESERCIZIO 120. Completa la seguente tabella.
| Proporzione | Antecedenti | Conseguenti | Medi | Estremi | Valore rapporto |
|---|---|---|---|---|---|
| 3 : 5 = 21 : 35 | 3 E 21 | 5 E 35 | 5 E 21 | 3 E 35 | 0,6 |
| 54 : 12 = 36 : 8 | |||||
| 7 : 21 = 9 : 27 | |||||
| 5/4 : 15/8 = 4 : 6 |
ESERCIZIO 121. Calcola il termine incognito delle seguenti proporzioni.
- A. 2692 : 24 = 3 : x.
- B. x : 0,6 = 0,8 : 1,3.
- C. 7/3 : x = 4/3 : 8/35.
- D. (1 - 5/12) : (5/6 + 1/3) = x : (9/8 - 5/8).
ESERCIZIO 122. Calcola il termine incognito delle seguenti proporzioni.
- A. (3/20 + 3/8) : x = (1 - 1/3) : (11/3 + 1/7).
- B. (1 + 1/4 - 1/8) : (5/8 + 1/4) = (5/8 + 1/2) : x.
- C. (4/5 + 1) : (3 - 1/5) = x : (2 + 1/3).
ESERCIZIO 123. Calcola il termine incognito delle seguenti proporzioni.
- A. (5/3 + 8/3 - 3) : x = x : (1 + 5/16 + 3/8).
- B. {5/2 : [1/2 * (3 + 1/3 : 5/3 - 14/5)]} : x = x : {3/11[(5 - 3/2) * 2/21 + 3/2]}.
- C. (70 - x) : 6 = x : 8.
- D. (5/6 - x) : (1 - 1/2) = x : (1/6 + 2/3).
ESERCIZIO 124. Calcola il termine incognito delle seguenti proporzioni.
- A. x : y = 5 : 3, con x + y = 24.
- B. (6 + 3/5) : y = (4/3 - 2/15) : x, con x + y = 13/4.
- C. (1/2 + 5/6) : (3/4 + 1/20) = x : y, con x - y = 1/3.
- D. x : 2/7 = y : 1/2 = z : 3/14, con x + y + z = 1/2.
ESERCIZIO 125. Per ciascuna funzione costruisci la tabella dei valori (almeno 5) e stabilisci se sono riferite a grandezze direttamente proporzionali, inversamente proporzionali o nessuno dei due casi.
- A. y = 5x.
- B. y = 1/2x.
- C. y = 2/3x.
- D. y = 1/x + 3.
- E. y = 6x + 1.
- F. y = 24/x.
- G. y = 4x.
- H. y = 18/x.
- I. y = 1/2x.
- J. y = 6/x.
- K. y = 5 + x.
- L. y = 3x + 2.
- M. y = 2/x.
- N. y = 2x.
- O. y = 2x - 1.
- P. y = 1/2x + 1.
- Q. y = 2x - 2.
ESERCIZIO 126. Osserva i grafici e rispondi alle domande:
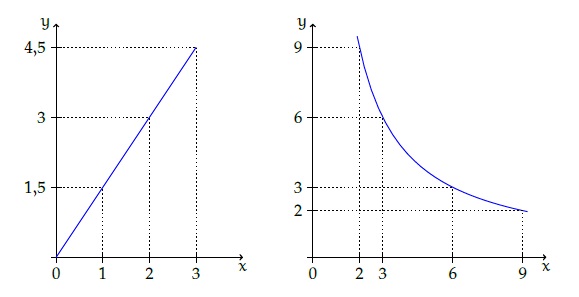
- A. Quale grafico rappresenta una funzione di proporzionalità diretta e quale di proporzionalità inversa?
- B. Qual è il coefficiente di proporzionalità? Del primo grafico è . . . . . . del secondo è . . . . . .
- C. Qual è la funzione? Del primo grafico è . . . . . . . . . del secondo grafico è . . . . . . . . .
ESERCIZIO 127. La tabella seguente riporta alcuni valori che esprimono il variare della grandezza y al variare di x:
| x | 1 | 2 | 3 | 4 | 6 | 8 | 12 | 24 |
|---|---|---|---|---|---|---|---|---|
| Y | 8 | 4 | 2 | 1 |
- A. Completa la tabella sulla base dei valori noti.
- B. Si tratta di grandezze direttamente o inversamente proporzionali?
- C. Qual è la legge che lega y a x?
- D. Rappresenta su un piano cartesiano questa relazione.
ESERCIZIO 128. La tabella seguente riporta alcuni valori che esprimono il variare dello spostamento s (espresso in km) in funzione del tempo t (espresso in ore) relativo a un corpo che si muove con velocità costante.
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| S | 7 | 21 | 35 | 49 | 56 |
- A. Completa la tabella sulla base dei valori noti.
- B. Si tratta di grandezze direttamente o inversamente proporzionali?
- C. Qual è la legge che lega s a t?
- A. Rappresenta su un piano cartesiano questa relazione.
Espressioni con le frazioni
[modifica]ESERCIZIO 129. Calcola il valore delle seguenti espressioni con addizioni e sottrazioni.
- A. 7/12 - (1/4 + 1/12).
- B. 5/16 - (1/8 - 1/16).
- C. 4/3 - (1/5 - 5/6).
- D. 6/7 + (4/7 - 1/14).
- E. (3/4 + 5/6) - 1/4.
- F. 7/4 - (3/8 + 1/4).
ESERCIZIO 130. Calcola il valore delle seguenti espressioni con addizioni e sottrazioni.
- A. 7/15 + (1/4 - 13/5) + (2 - 1/3) + (5/3 - 13/12.
- B. 4/5 - [3/5 - (1/3 + 1/6)] - (8/20 + 1/5).
- C. 3/2 - 1 + {2 + [1/2 + 5 - (4/3 + 1)] + 1/10} + 1 + 7/2.
- D. (4/3 + 4/5 + 2/3) - (21/9 - 8/6) + (9/5 - 10/15) - (9/5 - 10/6) - 4/5.
- E. 1/2 + [(7 - 3/2) + (5/3 - 5/2) + (3/4 - 1/3 - 5/6 - 1/2) + 9/4] - 1/4.
ESERCIZIO 131. Calcola il valore delle seguenti espressioni con addizioni e sottrazioni.
- A. 2/3 - [1/2 - (- 1/6 + 1/4)] - 2 - {- 5/2 - [1/2 + (5/3 - 1) - 2]}.
- B. [(1/2 - 7/6 + 1/5) + 121/60] - [179/40 - (7/6 - 3/8 + 1)] + 16/10 - (5/12 - 1/6).
- C. - 5/2 + {- 3/2 + [7/5 + 13/90 + (1/2 + 2/5 - 1/15) + (4 - 10/9)]}.
- D. [5/2 + (3/4 + 6/5)] - (6 - 7/20) + {3 + [7/20 + (9/20 + 5)]}.
- E. [(1/3 - 11/4 + 3) - 5/12] + {(1/15 - 9/10 + 1/2) + [5/2 - (5/6 - 3/8) - 2]}.
ESERCIZIO 132. Calcola il valore delle seguenti espressioni.
- A. (- 1 + 1/2) : (3/2 + 5/4).
- B. (- 2/3 + 1/2) * (1/2 - 3/4).
- C. 1/2 * (- 1/4 + 3/2) : (3/2 - 3/4).
- D. 1/3 - (2/3 - 5/6) + 3/2 - [3/4 - (7/30 - 4/5) + 5/6].
ESERCIZIO 133. Calcola il valore delle seguenti espressioni.
- A. [4/5 : (- 1/5)] * [5/12 : (- 4/3)].
- B. [(- 3/4 - 13/8) (1 - 9/23) + (- 7/2 - 1) (-1 - 1/23)] (-3 + 5/2).
- C. [2/5 (3 - 2/3 * 15/4)] * [(5 - 3/4) : 17/15 - 2/3 + (2/3 - 1/5) : 14/5].
- D. [(3/16 + 1/24) * 2 - (1 - 3/8) : 3] : [(4/5 - 1/3) * 3 + 12/5 : 4].
ESERCIZIO 134. Calcola il valore delle seguenti espressioni.
- A. 5/6 - 2/3 * 12/5 + 3/2 * [3/4 * (12/7 - 5/2) + 5/6].
- B. 5/6 * 2/3 * 12/5 - 3/4 : [0,75 - 5/6].
- C. 1/3 : (3/2 - 2/3) + 1/6 - 1/15.
- D. - (3/4 + 1,4) * (2/3 - 3/8) + 6/5.
ESERCIZIO 135. Calcola il valore delle seguenti espressioni.
- A. (2/3 - 7/6) - (1 + 5/6) : (2 - 1/3).
- B. (5/3 - 7/2) * 4/5 + [(1/3 - 1/15) * 5/2]2.
- C. 63/55 * 44/45 + 14/75 * 15/35 + 2/25 * 10 - 16/25 : 3/5 + 1/15.
- D. {[(1/2 - 2/3) : (5/6 - 5/12) * 1/2 + 3/4] : 1/4} - 2/3 * (-0,6).
ESERCIZIO 136. Calcola il valore delle seguenti espressioni.
- A. (3/2 - 2 - 1/4) - (1/2 - 5/4).
- B. (1/3 - 3) - [(- 1/2 + 2) + (9/2 - 1)].
- C. (5/6 - 3/4)(- 1/20 - 1/10).
- D. 1/2 (- 3/8) 4/3 + 1/4.
ESERCIZIO 137. Calcola il valore delle seguenti espressioni.
- A. [(3 - 1/2) - (1/5 - 1/2)][(1 + 2/3) - 1/2].
- B. (1/3 + 1/6 - 1/2) : (3/4 - 1/2).
- C. (6 - 2/3 + 1/5) : (2/3 - 1 - 1/5).
- D. [(2/3 - 1/5 + 1)(3/4 - 1/2)] : (4/3 - 1).
ESERCIZIO 138. Calcola il valore delle seguenti espressioni.
- A. 4/5 - 27/7 * 1/12 + 8/21 : 8/6 + 13/2 * 1/7 - 9/14 + 1/7 - 12/25 : 3/5.
- B. [(1/3 - 1/7) * 7/2 - (10/18 - 7/15) : 2/9] : 14/15 * 1/4 + 1.
- C. [(4/3 - 1/10) : 37/5 + (1/2)2 - 1/3]2 : [(1/2)2 - (1/3)2 + (1/4)2 - (1/6)2 + (5/12)2].
- D. (3/5 - 1/4) * (7/5 + 3/4) - (2/3 - 5/4 * 3/7) : 2/14 - 1/400.
ESERCIZIO 139. Calcola il valore delle seguenti espressioni.
- A. (3 - 18/5 - 5/6) * (- 9/4 + 3/4) - 22/3 + 1/60.
- B. (3/5 - 1) - (1/8 + 7/5 - 17/20) + (7/6 - 2/5) : 4/15 - (3/2 - 5/2 : 1/5) : 22/17 - 3/10.
- C. 19/3 * (3/5 + 3/2 - 2) : (3/10 - 1,25) - (1/2 - 1/5 - 1) + 3/2 * (- 3/10 + 1/2) * (- 5/3)2.
- D. [(1 + 1/2) : 3 - (2 + 3/2) + 1] + (3 - 3/4) + (1/3 + 3/2) - 1 (- 2 + 3/2)2.
ESERCIZIO 140. Calcola il valore delle seguenti espressioni.
- A. [2/3 - (- 1/4 + 2/5)] - [3/5 - (3/4 - 1/3)].
- B. 2 - [3 + 1 - (2 - 1/2)] - (- 2 - 1/2) * (1/2 - 3/4 + 1/6) : (- 1/2).
- C. (8/3 - 1/6)−1 - (1/2 - 3/8) + 10/8 * (5/7)−2 + (1/3)−3 * 1/62 ;
- D. {(2/5)4 * [(2/5)8 : (2/5)3]2}2 : [(2/5)3 * 2/5 * (2/5)3]4.
Esercizi riepilogativi
[modifica]ESERCIZIO 141. Calcola il valore delle seguenti espressioni.
- A. (4/5 : 2/3 + 1/5) * 3/2 + 3/4 : [5/8 + 1/3 : (3/5 - 1/3)] - 1/4 : 1/2.
- B. (5/2 + 1/15) : (2 + 1/5) + (1 - 7/36) : (2 - 7/18) + [1 - 1/3 - (1 - 9/14) : 10/7] : 5/2.
- C. (3/5 - 1/4) 5/14 - (4/5 - 1/3) : 4/5 - 1/8 + (2/3 + 3/4) 5/18.
- D. {- 2/3 [- 4/5 (-1 - 1/4)]} - (-2 + 1/2) * {- 2/3 [- 5/4 (-1 + 1/5)]} (1 + 1/2).
ESERCIZIO 142. Calcola il valore delle seguenti espressioni.
- A. (-2 + 3/7 + 8)[3 - (6 + 1/2)] * 1/9 - (-1 + 1/3)(1 + 1/2)(- 3/7 + 3)(- 1/4).
- B. [(3/8 + 3/5)(-1 + 8/13) + 1/8 - 1/4](1 - 1/3 + 1/6).
- C. {5/6 - [3/4 + (2/3 - 3) + 2/3 - 2]} : {3/4 - [- 1/2 - (3/4 - 1) + 3/8]}.
- D. 1 + 3/4 {- 2/3 - [5/6 + (3/2 - 1) : (1/2 + 2) - 3/2] : (- 3/2)} (1 + 1/3).
- E. 15 [(2/3 - 1/2 + 2/5) : (- 1/2 - 1/3)] - 17 [(1/5 - 3/10) : (1/2 - 1/3)].
ESERCIZIO 143. Calcola il valore delle seguenti espressioni.
- A. 1 - [(3/2)3 * (3/2)2 : (3/2)4 - (4/5)3 : (4/5)3 + (1/3)4 : (1/3)3].
- B. (1/4)−2 - (1/2)−2 + 22/3 * (2/3)−3 - - 24.
- C. {[1/6 + 1/2 : (6/8 + 1 - 3/4)]3 * (3/5 - 3/8) + 3/5} : 1/5.
- D. {1/2 + 15/2 : [1/2 : (1 - 3/4) + 1]} * [(1/3)5 : (1/3)4]2.
ESERCIZIO 144. Calcola il valore delle seguenti espressioni.
- A. [2/3 (- 3/4)(- 1/2)3]2 : [(1/2)2]3.
- B. [(- 1/2)3(- 1/5)2] : (- 3/5 - 1/2)2.
- C. [(2 - 2/3)2 : (-3)3] : (- 1/16) - 13/35.
- D. [(- 1/2)3(- 2/3)(- 3/4)]2 : [(- 1/2)3]2.
- E. {(- 1/3)5[(- 1/3)2]2 : [(- 1/3)3]3}4.
- F. []4 : [(- 1/5)3(- 1/5)2]2.
ESERCIZIO 145. Calcola il valore delle seguenti espressioni.
- A. {[(5/4)2 : (1/2)] * [(1/5 + 1/10 + 1/20) * 4/5] * 1/14}2 : (1 - 5/6 * 3/10)2.
- B. [(0,4 - 1)2 : 0,01 - (- 2/3)−2] * (- 1/2)−4.
- C. 7/15 {(9/4 + 3/4 * 1/2 - 11/16 * 1/2 + 1/8) : [(4/7 + 5/4) : 17/7]} * 9/5.
- D. (2 + 1/2)2 : (2 - 1/2)−2 + [(2 + 1/3) * (7/3)−2]−1.
ESERCIZIO 146. Calcola il valore delle seguenti espressioni.
- A. [(3 + 1/2 - 5/3) * (1/2)2] : {3/2 - [2/3 + (2/11 + 5/22 + 7/33) : 82/33 + 1/12]5}3 : 1/4.
- B. {[(8/3)10 : (8/3)6]2 * [(8/3)8 : (8/3)3]} : (8/3)11.
- C. (1 + 3/2)2 * (2 - 5/2)−2 * [(1/2)2]−2.
- D. (1/3 - 1) - (1/6 - 1/4) * 6/5 - (2/9 - 1/5) * 3 - 1/30.
ESERCIZIO 147. Calcola il valore delle seguenti espressioni.
- A. : .
- B. 8,75 * (2/5 - 0,2) * {[2 - 1,6 - (0,2 + 2/3)] * (1/7 - 17/4)} - 2/3 * (2 - 1/2) + 7,5 - 0,3.
- C. [(7/5 - 1/2)2 : (9/10)2 - (1 + 2/3 - 2)2]2 : (10/9)2 - (1 + 8/5 - 1/25).
- D. (1/6 + 0,1) * 0,16 * (1 - 1,01)−1.
ESERCIZIO 148. Calcola il valore delle seguenti espressioni.
- A.
- B. (4/3 - 2)(- 1/2) : [5/7 (2/5 - 1/6) + (2 + 2/5)(3/4 - 4/3 + 1/2)] : 11/6.
- C. (1 - 1/2)−2 * [(1 + 1/2)2]−2 : (5/2 - 2)−3.
ESERCIZIO 149. Calcola il valore della seguente espressione.
- {[(1 - 3/5)3 : (2/5)4] : (3/5 - 1)2}6 : {[(4/5 - 2/5)4 * (7/5 - 1)2]2 * [(1 - 3/5)5 : (1/5 + 1/5)4}2}2.
ESERCIZIO 150. Calcola il valore delle seguenti espressioni.
- A. (1 + 1/2)[1/4 + (1 - 2/5) : (2 - 1/2)2] : [(2 + 2/5) : (1 - 3/5)2 + (1 + 1/2) : 3].
- B. [3/16 (5 - 3/2) : (1 - 1/4 - 3/16)] * 4/7 (2 + 1/2)2 - (1 + 1/2)2 + 1/12.
- C. (-1)2 - 22 + 2 {[- 2/3 (- 3/4)(- 1/2)3]2 : [(- 1/2)2]3}.
- D. [(8/3 - 7/4 - 1/2)2 6/5 - (5/6 + 2/3 + 9/4)(11/6 - 13/30 : 1/3 - 2/5)2] : 3/2 + 23/30.
ESERCIZIO 151. Calcola il valore della seguente espressione.
- [(2/5 - 25/3 * 1/10 + 3/4 : 3/2)2(3/10 * 1/3 + 77/6 : 11/3 + 7/5)3 - (3/4)4 : (3/4)2(2/3)3] : {[(1/10 - 3/20 + 2/25) : 2/5 + (8/35 - 1/4) 7/3] : 3/20 * 7/3}.
ESERCIZIO 152. Calcola il valore delle seguenti espressioni.
- A. (1/5 - 1/4)(- 1 - 1/3) + [(1 + 4/3) * (4 - 9/2)] * 3/4 + 3 - (2/27 * 9/10 - 1/10) - 9/40.
- B. [0,625 + 4,5 * (0,75 - 0,6)] : [0,875 + 0,75 * (2,5 - 2,3)].
- C. {3 - [0,6 - [0,16 + 5/12)] : 0,25}2 * (0,6 - 0,625).
- D. (12/9 - 1)2 * (2/81 : 3)−1 * 1/2 + (7/4)3 * [- (4/3 - 1/3)3 * (5/49 - 3/147)] - .
ESERCIZIO 153. Calcola il valore delle seguenti espressioni.
- A. .
- B. .
- C. .
- D.
ESERCIZIO 154. Calcola il valore delle seguenti espressioni.
- A. (1/5)2 - (1/6)−1 - + ()−2 -4−2.
- B. [0,16 + (0,136 + 0,416 - 0,227) : 0,390] : [0,36 + 2,25 * (0,5 - 0,27)].
- C. .
- D. 0,162 + [1,5 : 1,52 + (1,6 - 0,5) : (2 - 0,3) + (0,6 + 0,5 - 0,2) * 0,75 : 5,8] * 0,6.
ESERCIZIO 155. Calcola il valore delle seguenti espressioni.
- A. {0,83 - [0,6 + (0,75 - 0,62 - (1 - 2,3 * 0,25))] + 0,6 : 0,8}: 1,027.
- B. Errore del parser (errore di sintassi): {\displaystyle \frac{1}{<math>\sqrt{3<sup>2</sup> + 4<sup>2</sup>}\quad} }\ </math> + Errore del parser (errore di sintassi): {\displaystyle \frac{1}{<math>\sqrt{13<sup>2</sup> + 12<sup>2</sup>}\quad} }\ </math> - .
- C. + .
- D. .
ESERCIZIO 156. Calcola il valore delle seguenti espressioni.
- A. .
- B. (1 + )−2 * (1 - )2 * (4 - 9/2)−3.
ESERCIZIO 157. Calcola il valore delle seguenti espressioni.
- A. [(2 + )−3 * ( - 1/8) * (- 3/10)−2]−2.
- B. - [(177 + 33/21) - (1 - 1/5 - 2/7)].
ESERCIZIO 158. Calcola il valore della seguente espressione.
- (7/6 - 5/4) : (1/12 - 1/2) - 3/10 + {[2 - (2 + 1/2 - 3/4 + 1/8) : (- 1/2)] * 2 - 7/10} * (- 2/3 + 1/2) + [1/3 + (1 - 1/4) : (- 9/2) + 1/15].
ESERCIZIO 159. Calcola il valore della seguente espressione.
- (- 3/2 - 1) * (- 3/2 + 1) + (3/4 - 2) * (- 3/4 - 2) * 4/11 + (2/3 - 3/4) - [1/9 - (3/2 - 2/3) : (9/4 + 1 + 2/3 - 1/6) + 2/3 : (9/4 - 9/4 + 1/3)] + (7/6 - 1)2.
ESERCIZIO 160. Calcola il valore della seguente espressione.
- [- (-1/5)2 : (3/5 - 1)−2] * (- 1 - 1/5)−2 * (- 2)−2 * 302 - {- [(- 3 - 1/4 + 13/4)2 : (-4)−2]}.
ESERCIZIO 161. Calcola il valore della seguente espressione.
- [- (-1)3 + (2/3 - 1)−2] * (- 1 - 1/7)−1 * (-1/5)2 + {- 1/2 * [(- 1 - 1/2)−2 * (- 3/2 - 1)2]−1 : (-5)−2}2.
ESERCIZIO 162. Calcola il valore della seguente espressione.
- 1 - (1/2 - 3/4)2 - [3/4 + (- 1/2)3 - 1 + 4/5] : [- (4/5)0 - (7/5 - 2)2] - 3/2 + [(- 4/5)−3]2 : (- 4/5)−5.
ESERCIZIO 163. Calcola il valore della seguente espressione.
- Errore del parser (funzione sconosciuta '\Frac'): {\displaystyle \Frac{[(20<sup>4</sup>/2<sup>4</sup>) * 3<sup>4</sup>]<sup>2</sup>}{30<sup>6</sup>}\ } - []3.
ESERCIZIO 164. Calcola il valore dell'espressione E = A - B, dove
- A = (((- 3/7)4 : (- 7/3)−2) * (3/7)−1)−2.
- B = ((3/7)−6 * (1 - 4/7)5)2.
ESERCIZIO 165. L'età di Paolo è i 5/11 di quella della madre che ha 44 anni. Quanti anni ha Paolo?
ESERCIZIO 166. L'età di Marco è 1/2 di quella di Paolo che è 1/3 di quella del padre che ha 54 anni. Quanti anni ha Marco?
ESERCIZIO 167. I 2/5 del libro che stiamo leggendo è la parte più noiosa. Le rimanenti 63 pagine sono invece le più avvincenti. Di quantepagine è formato il libro?
ESERCIZIO 168. Gli alunni del primo e del secondo anno di una scuola media sono rispettivamente i 3/7 e i 2/7 del totale. Sapendo che gli alunni che frequentano la terza media sono 54, quanti sono tutti gli alunni della scuola?
ESERCIZIO 169. Al supermercato ho speso 7/10 della somma di denaro che possedevo; successivamente ho incassato un credito uguale ai 13/20 della somma iniziale e ho speso 2/15 sempre della somma iniziale per un rifornimento di benzina. Sapendo che sono rimasto con 220,50 euro, quale somma di denaro possedevo inizialmente?
ESERCIZIO 170. In una fattoria ci sono vitelli, capre e animali da cortile per un totale di 75 capi. I vitelli sono i 2/5 di tutti gli animali, mentre le capre sono i 2/3 degli animali da cortile. Quanti vitelli, capre e animali da cortile ci sono?
ESERCIZIO 171. Tre casse pesano complessivamente 220 kg; la seconda pesa 1/2 della prima e la terza pesa 1/3 della seconda. Calcola il peso di ciascuna cassa.
ESERCIZIO 172. Tre operai devono eseguire un lavoro. Il primo da solo lo farebbe in 12 giorni, il secondo in 18 giorni e il terzo in 36 giorni. Lavorando insieme, in quanti giorni i tre operai potrebbero eseguire tutto il lavoro?
ESERCIZIO 173. Un collezionista vende i 3/7 della sua collezione costituita da 385 pezzi. Quanti pezzi gli rimangono?
ESERCIZIO 174. In un terreno agricolo sono stati piantati ulivi e mandorli per 266 alberi complessivi. Se gli ulivi sono i 4/10 degli alberi di mandorle, quanti sono gli ulivi e i mandorli.
ESERCIZIO 175. Il prezzo di copertina di un libro è di 29 euro; quanto verrà pagato con uno sconto del 15%?
ESERCIZIO 176. Su 1020 alunni di una scuola, 153 sono stati respinti; qual è la percentuale dei promossi?
ESERCIZIO 177. In una classe gli alunni biondi sono il 40% del totale, mentre i restanti sono castani. Tra tutti gli alunni biondi, il 75% sono femmine. Sapendo che nella classe il numero di femmine è uguale al numero dei maschi, qual è la percentuale di maschi castani sul totale degli alunni della classe? (Olimpiadi della Matematica 2012).
ESERCIZIO 178. Al 22 novembre 2012 il prezzo della benzina è dato per il 35% dal costo del prodotto, che è formato a sua volta da diverse voci (petrolio, raffinazione, costi di distribuzione, ecc.); il costo del petrolio costituisce oggi il 24% del costo del prodotto. Sapendo che il primo gennaio 2013 il prezzo del petrolio aumenterà del 10% e gli altri costi rimarranno invariati, di quanto aumenterà il prezzo della benzina in tale data? (Olimpiadi della Matematica 2012).
ESERCIZIO 179. I 4/5 degli alunni di una classe sono stati promossi senza debiti formativi. Sapendo che gli alunni promossi con debito formativo sono 1/6 dei promossi senza debiti,la frazione dei non promossi rispetto all'intera classe è . . . (Olimpiadi della Matematica 1999).
ESERCIZIO 180. Se aumentiamo la lunghezza della base di un rettangolo del 30% e quella dell'altezza del 50% l'area aumenta del . . . (Olimpiadi della Matematica 2000).
ESERCIZIO 181. La differenza di età fra Marco e Antonio è di 18 anni e l'età di Marco è i 7/4 di quella di Antonio. Quanti anni hanno Marco e Antonio?
ESERCIZIO 182. Un oggetto è costituito da una lega di zinco e rame. Il suo peso è di 280g e la percentuale di rame è il 20%. Quanti grammi di zinco contiene?
ESERCIZIO 183. Mario va in pizzeria e, nell'attesa di essere servito, conta le persone che vi si trovano: gli uomini sono i 5/9 delle donne, queste superano gli uomini di 8 unità, infine vi sono 17 bambini. Quante persone ci sono in tutto? Quanti sono gli uomini e le donne?
ESERCIZIO 184. Gino compra un'auto da € 5400. Paga i 4/9 in contanti ed il resto in 5 rate. Qual è l'ammontare di ogni rata? A quale frazione corrisponde ogni rata?
ESERCIZIO 185. Il serbatoio di una macchina contiene benzina per i 3/4 della sua capacità. Dopo aver consumato i 2/3 della benzina che c'è, si fa un pieno aggiungendone 66 litri. Qual è la capacità del serbatoio?
ESERCIZIO 186. Un misurino contiene 1/8 di kg di farina. Quanti misurini di farina sono necessari per riempire un sacchetto di 5 kg?
ESERCIZIO 187. Due gruppi di scavatori scavano una galleria, ciascun gruppo comincia da una delle due parti opposte; se fino a oggi hanno scavato rispettivamente 5/9 e 3/7 dell'intera galleria e restano ancora da scavare 2m, quanto è lunga l'intera galleria?
ESERCIZIO 188. L'aria è composta per 39/50 di azoto e per 21/100 di ossigeno, la parte rimanente è composta da gas diversi. Quale frazione di aria occupano tutti gli altri gas?
ESERCIZIO 189. Luca ha pagato la tassa scolastica in ritardo, ha pagato € 56,16 compresa la mora del 4% per il ritardo nel pagamento. Quanto avrebbe dovuto pagare senza mora?
ESERCIZIO 190. In un'azienda 3/10 degli impiegati sono addetti contabilità. Qual è la percentuale degli addetti contabilità rispetto a tutti gli impiegati azienda?
ESERCIZIO 191. A un gruppo di 200 intervistati è stato chiesto quale quotidiano leggono. Le risposte sono state le seguenti:
- 90 Leggono “La Repubblica”.
- 70 Leggono “Il Corriere della sera”.
- 30 Leggono “La stampa”.
- 10 Leggono “La gazzetta dello sport”.
Trasforma in percentuali i dati ottenuti.
ESERCIZIO 192. A un concorso si sono presentati 324 candidati. 22 hanno superato il concorso. Qual è stata la percentuale dei candidati che non hanno superato il concorso?
ESERCIZIO 193. Un'auto usata è stata acquistata a € 11800 in questo modo: il 5% come caparra per la prenotazione, il 20% al momento della consegna e il resto in 12 rate di pari importo. Qual è l'importo della rata?
ESERCIZIO 194. Un gestore di un bar acquista i cornetti a € 0,60 e li rivende a € 0,75. Qual è la percentuale di guadagno sul prezzo di acquisto?
ESERCIZIO 195. In un supermercato si vende il pomodoro pelato a € 0,60 in confezioni da 250g e a € 1,00 in confezioni da 500g. Qual è la percentuale di sconto che usufruisce chi compra la confezione da mezzo chilo?
ESERCIZIO 196. In una piscina contenente 2800m3 di acqua si devono aggiungere 15 litri di cloro. Quanto cloro occorre per 1000m3 di acqua?
ESERCIZIO 197. La somma di due segmenti misura 34 cm, sapendo che le loro lunghezze sono in proporzione con 3/2, calcola la loro lunghezza.
ESERCIZIO 198. Gli angoli interni di un triangolo hanno misure proporzionali ai numeri 1, 3, 5. Ricordando che la somma degli angoli interni di un triangolo misura 180°, calcola le misure degli angoli.
ESERCIZIO 199. Un televisore a 16/9 ha la base di 18 pollici. Quanti pollici misura l'altezza?
ESERCIZIO 200. Per preparare una torta bisogna mettere 3 parti di zucchero ogni 4 parti di farina. Se si utilizzano 500g di farina, quanto zucchero bisogna utilizzare?
ESERCIZIO 201. Un negoziante, durante il periodo di Natale, aumenta tutti i prezzi del 10%. Se il prezzo iniziale di un paio di scarpe era di € 70,00 qual è ora il suo prezzo? Dopo le feste, il negoziante abbassa i i prezzi del 10%. Quanto costano ora le scarpe?
ESERCIZIO 202. Al cinema “Pegaso” hanno deciso di aumentare il biglietto del 10%; il numero degli spettatori è calato, però, del 10%. È stato un affare? Spiega perché.
ESERCIZIO 203. Anna entra in una cartoleria e compra due penne, di cui una costa il doppio dell'altra; riceve lo sconto 15% sulla penna più costosa e del 40% su quella meno costosa. Qual è lo sconto che riceve complessivamente?
ESERCIZIO 204. Pierino oggi ha incrementato il suo capitale del 10%. Se anche domani l'incremento sarà del 10%, quanto sarà l'incremento totale in percentuale?
ESERCIZIO 205. Tizio ha perso il 20% dei suoi soldi; quanto dovrà guadagnare, in percentuale, per recuperare?
ESERCIZIO 206. Un paio di scarpe scontato del 20% costa € 40. Quanto costava prima dello sconto?
ESERCIZIO 207. Per pavimentare una piazza 8 operai impiegano 10 giorni lavorando 8 ore al giorno; quanti giorni impiegherebbero 5 operai se lavorassero 6 ore al giorno?
ESERCIZIO 208. Pierino si reca in un negozio di giocattoli, dove ne acquista uno. A Pierino vengono offerti due tipi di sconti, uno del 10% e uno del 35%. In quale ordine converrà ricevere i due sconti? Spiega il motivo.
ESERCIZIO 209. Una tariffa telefonica ha un costo di 10 cent al minuto per i primi 5 minuti di conversazione. Per i minuti successivi aumenta del 5%. Dopo 15 minuti di conversazione aumenta del 20% del costo iniziale. Quanto si spende se si effettua una telefonata di 20 minuti?
ESERCIZIO 210. Un ingegnere incassa per la realizzazione di un progetto una certa somma. Di essa il 20% deve essere restituita allo stato come IVA e della parte rimanente il 40% deve essere pagata come tasse. Qual è la percentuale della somma che rimane all'ingegnere?
ESERCIZIO 211. Nel paese di Vattelapesca il 20% degli abitanti è europeo il restante 80% è asiatico. La lingua inglese è parlata dal 50% degli europei e dal 40% degli asiatici. Se a Vattelapesca np5930 persone parlano inglese, quanti sono gli abitanti di Vattelapesca?
ESERCIZIO 212. Un liquido viene filtrato con un primo filtro che toglie il 40% delle impurità. Successivamente viene filtrato con un secondo filtro che toglie il 30% delle impurità. Infine viene filtrato con un terzo filtro che elimina il 50% delle impurità. Quale percentuale complessiva delle impurità è stata eliminata?
ESERCIZIO 213. Una prova di ammissione consiste di due test. Solo i 2/3 dei candidati superano il primo test e 1/5 di quelli che hanno superato il primo test superano anche il secondo. Qual è la percentuale di candidati che hanno superato tutti e due i test?
ESERCIZIO 214. L'acquisto di un'auto può essere fatto con due tipi di pagamento: pagando l'intero importo di € 23000 all'acquisto il 1° gennaio 2011; oppure dividendo il pagamento in tre rate annuali da € 8000, da pagare il 1° gennaio 2011, il 1° gennaio 2012 e il 1° gennaio 2013. Avendo tutto il denaro su un conto corrente bancario a un interesse annuo del 3% quale forma di pagamento è più vantaggiosa? Di quanto?
ESERCIZIO 215. Una forte influenza ha colpito il 60% dei bambini di età inferiore o uguale a 10 anni e il 15% delle persone di età maggiore. Se la percentuale di persone che si sono ammalate di questa influenza è stata del 20%, qual è la percentuale di bambini in quella popolazione?
ESERCIZIO 216. Una maglietta costava 65000 lire prima dell'entrata in vigore dell'euro e dopo costava € 40. Di quanto è aumentato in %, il prezzo della maglietta? Si tenga conto che 1 euro valeva 1936,77 lire.
ESERCIZIO 217. Una ragazza, di 46 kg, va dal dietologo, che le consiglia di restare entro il 5% del peso attuale. Tra quali valori può oscillare il suo peso?
ESERCIZIO 218. Per raccogliere le foglie cadute nel cortile della scuola, Mario impiega 6 ore, Marco 10 ore, Matteo 15 ore. Se i tre si mettessero a lavorare insieme, in quante ore pulirebbero il cortile?
ESERCIZIO 219. Una certa bevanda è ottenuta mescolando 1 parte di sciroppo con 5 parti di acqua. Per errore Adolfo ha mescolato 5 parti di sciroppo con 1 di acqua, ottenendo 3 litri di miscuglio. Aggiungendo una opportuna quantità di acqua, Adolfo può ottenere una bevanda in cui sono rispettate le proporzioni stabilite? Quanti litri di acqua deve aggiungere?















![{\displaystyle {\frac {{[1/2-(2-11/4)]:(-3,5)}*(1-4/5):7<sup>-2</sup>}{(-1/3)<sup>-3</sup>(-3)<sup>2</sup>(-1)<sup>2</sup>:(-3)<sup>2</sup>}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc629b0ff29dc9a7df75867de389e3fdb39e03f8)

![{\displaystyle {\frac {[(9/12+10/4):26/4+(10/8-21/18):10/12][9/15+2-10/6):35/45]}{[(15/25-2/6)9/12+(4/15-11/45)5]:7/9}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/de4e4b84bff17d8e6b61cbe111488902c1296785)
![{\displaystyle {\frac {(5/9-2/3)+(1/3+5/4:15/3):[(4/7)<sup>3</sup>:(4/7)<sup>3</sup>+(1/4)<sup>2</sup>+(1/2)<sup>2</sup>]}{[(5/2)<sup>2</sup>1/3:5/2+1]:(3/2-1/8)-(7/3-2)}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b34b363292f1b7c68afb7a41dbf108ffa3fde77e)
<sup>2</sup>}{[3/2+6/5-(1-4/5)](1-1/5)<sup>2</sup>}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d79c2cf586f8680bee5ce20a218d2171475bc8e)
![{\displaystyle {\frac {1/6[(1+1/2)<sup>2</sup>-(1-1/3)<sup>2</sup>]+[(1-1/2)<sup>2</sup>+(1-2/3)<sup>2</sup>]}{[(1+1/2)<sup>2</sup>-(1-1/3)<sup>2</sup>](1/2-1/3)+(1-1/2)<sup>2</sup>-(1-2/3)<sup>2</sup>}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d886957de8b3d2fcafd3ea5f1659b09288877f2a)






![{\displaystyle {\sqrt {1/9*{[11/3-(1/3-1/4)]:[(2-7/4)+10/3]}}}\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0580a94a8c43ee233ba62f35baee24217602c839)
![{\displaystyle {\sqrt {{[(5/4)<sup>2</sup>:(1/4)<sup>2</sup>][(1/5+1/10+1/20)*4/5]*1/4}<sup>2</sup>:(1-5/6*3/10)<sup>2</sup>}}\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb41203c2f94108b7bd552b102b3caf2c25362ff)




![{\displaystyle {\frac {[-(9/4+9/5)-1/20]*(11/4-5/2)}{1-[1-(-17/7)]-(-1+2/7-1/14)}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a3eb5e3b878617a914c70631e80ccb7582175a7)
