I seguenti esercizi riguardano la Dinamica del corpo rigido studiata nella Lezione 6 di Meccanica.
Una scala di massa
m
{\displaystyle m\ }
l
{\displaystyle l\ }
μ
s
{\displaystyle \mu _{s}\ }
θ
{\displaystyle \theta \ }
M
{\displaystyle M\ }
(dati del problema
m
=
10
k
g
{\displaystyle m=10\ kg\ }
M
=
80
k
g
{\displaystyle M=80\ kg\ }
μ
s
=
0.5
{\displaystyle \mu _{s}=0.5\ }
θ
=
22.5
o
{\displaystyle \theta =22.5^{o}\ }
→ Vai alla soluzione
Una fune sostiene una trave orizzontale di massa
m
/
2
{\displaystyle m/2\ }
l
=
8
m
{\displaystyle l=8\ m\ }
m
=
900
k
g
{\displaystyle m=900\ kg\ }
B della trave, quindi non può scorrere, e forma un angolo
θ
=
40
o
{\displaystyle \theta =40^{o}\ }
Determinare a ) la tensione della fune tra il muro e l'asta ; b ) la componente normale esercitata dalla trave sulla parete ; c ) il coefficiente minimo di attrito statico tra parete e trave, in maniera che la trave rimanga bloccata alla parete.
→ Vai alla soluzione
Determinare il centro di massa di un mezzo anello di raggio
R
{\displaystyle R\ }
m
{\displaystyle m\ }
→ Vai alla soluzione
Determinare il centro di massa di un quarto di anello di raggio
R
{\displaystyle R\ }
m
{\displaystyle m\ }
→ Vai alla soluzione
Determinare il centro di massa di un mezzo disco di raggio
R
{\displaystyle R\ }
m
{\displaystyle m\ }
→ Vai alla soluzione
Determinare il centro di massa di un quarto di disco di raggio
R
{\displaystyle R\ }
m
{\displaystyle m\ }
→ Vai alla soluzione
R
=
70
c
m
{\displaystyle R=70\ cm\ }
R
/
2
{\displaystyle R/2\ }
→ Vai alla soluzione
Un disco di massa
m
=
3
k
g
{\displaystyle m=3\ kg\ }
R
=
20
c
m
{\displaystyle R=20\ cm\ }
F
=
20
N
{\displaystyle F=20\ N\ }
R
{\displaystyle R\ }
θ
=
30
o
{\displaystyle \theta =30^{o}\ }
Determinare a) la tensione del filo; b) il coefficiente di attrito statico minimo che permette l'equilibrio. c) Se la forza viene applicata, più in alto ad altezza
x
{\displaystyle x\ }
x
{\displaystyle x\ }
→ Vai alla soluzione
Una asta rigida di massa trascurabile ha agli estremi due sfere piene di ferro
ρ
F
e
=
7.8
g
/
c
m
3
{\displaystyle \rho _{Fe}=7.8\ g/cm^{3}\ }
R
1
=
2.5
c
m
{\displaystyle R_{1}=2.5\ cm\ }
R
2
=
4
c
m
{\displaystyle R_{2}=4\ cm\ }
C
{\displaystyle C\ }
ℓ
/
2
=
5
c
m
{\displaystyle \ell /2=5\ cm\ }
C
{\displaystyle C\ }
Il filo si spezza e il sistema incomincia a ruotare, determinare c) l'accelerazione angolare del sistema all'istante iniziale del moto; d) la velocità angolare quando l'asta è verticale.
→ Vai alla soluzione
→ Vai alla traccia
Detto
A
{\displaystyle A\ }
B
{\displaystyle B\ }
x
{\displaystyle x\ }
y
{\displaystyle y\ }
B
{\displaystyle B\ }
f
B
y
−
m
g
−
M
g
=
0
{\displaystyle f_{By}-mg-Mg=0\ }
da cui:
f
B
y
=
(
m
+
M
)
g
=
882
N
{\displaystyle f_{By}=(m+M)g=882\ N\ }
Lungo la direzione orizzontale:
f
A
x
+
f
B
x
=
0
{\displaystyle f_{Ax}+f_{Bx}=0\ }
Detta
l
1
{\displaystyle l_{1}\ }
A
{\displaystyle A\ }
0
{\displaystyle 0\ }
l
{\displaystyle l\ }
B
{\displaystyle B\ }
M
g
l
1
sin
θ
+
m
g
l
2
sin
θ
−
f
A
x
l
cos
θ
=
0
{\displaystyle Mgl_{1}\sin \theta +mg{\frac {l}{2}}\sin \theta -f_{Ax}l\cos \theta =0\ }
da cui:
f
A
x
=
M
g
l
sin
θ
+
m
g
l
2
sin
θ
l
cos
θ
=
tan
θ
g
(
M
l
1
l
+
m
2
)
=
−
f
B
x
{\displaystyle f_{Ax}={\frac {Mgl\sin \theta +mg{\frac {l}{2}}\sin \theta }{l\cos \theta }}=\tan \theta g(M{\frac {l_{1}}{l}}+{\frac {m}{2}})=-f_{Bx}\ }
Che è massima quando:
l
1
=
l
{\displaystyle l_{1}=l\ }
cioè per:
f
B
x
=
−
tan
θ
g
(
M
+
m
2
)
=
−
345
N
{\displaystyle f_{Bx}=-\tan \theta g(M+{\frac {m}{2}})=-345\ N\ }
La condizione di equilibrio è verificata infatti:
|
f
B
x
|
≤
|
μ
s
f
B
y
|
=
440
N
{\displaystyle |f_{Bx}|\leq |\mu _{s}f_{By}|=440\ N\ }
→ Vai alla traccia
a)
Imponendo che sia nullo il momento totale delle forze, rispetto all'estremo
sulla parete:
m
g
l
+
m
2
g
l
2
−
T
l
sin
θ
=
0
{\displaystyle mgl+{\frac {m}{2}}g{\frac {l}{2}}-Tl\sin \theta =0\ }
segue che:
T
=
m
g
sin
θ
(
1
+
1
4
)
=
17
⋅
10
3
N
{\displaystyle T={\frac {mg}{\sin \theta }}\left(1+{\frac {1}{4}}\right)=17\cdot 10^{3}\ N\ }
b)
La componente normale della reazione vincolare della parete alla compressione vale:
N
=
T
cos
θ
=
13
⋅
10
3
N
{\displaystyle N=T\cos \theta =13\cdot 10^{3}\ N\ }
c)
Le forze verticali agenti sulla trave ad esclusione della reazione vincolare sono:
F
y
=
−
m
g
−
m
g
2
+
T
sin
θ
=
−
m
g
4
=
−
2.2
⋅
10
3
N
{\displaystyle F_{y}=-mg-{\frac {mg}{2}}+T\sin {\theta }=-{\frac {mg}{4}}=-2.2\cdot 10^{3}\ N\ }
Quindi, dovendo essere:
μ
s
N
+
F
y
=
0
{\displaystyle \mu _{s}N+F_{y}=0\ }
Il minore coefficiente di attrito statico che garantisce il blocco della trave vale:
μ
s
=
−
F
y
N
=
0.17
{\displaystyle \mu _{s}=-{\frac {F_{y}}{N}}=0.17\ }
→ Vai alla traccia
Scegliamo l'origine e gli assi come in figura.
La densità lineare di massa vale:
λ
=
m
π
R
{\displaystyle \lambda ={\frac {m}{\pi R}}\ }
Mentre l'elemento di lunghezza infinitesima, assunto come variabile l'angolo
θ
{\displaystyle \theta \ }
d
l
=
R
d
θ
{\displaystyle dl=Rd\theta \ }
Quindi:
d
m
=
λ
d
l
=
m
π
R
R
d
θ
=
m
π
d
θ
{\displaystyle dm=\lambda dl={\frac {m}{\pi R}}Rd\theta ={\frac {m}{\pi }}d\theta \ }
Tale generico elemento di trova nel punto di coordinate:
(
x
′
,
y
′
)
=
(
R
sin
θ
,
R
cos
θ
)
{\displaystyle (x',y')=(R\sin \theta ,R\cos \theta )\ }
Quindi:
x
C
M
=
∫
−
π
/
2
+
π
/
2
x
′
d
m
m
=
∫
−
π
/
2
+
π
/
2
R
sin
θ
m
π
d
θ
m
=
R
π
[
−
cos
θ
]
−
π
/
2
+
π
/
2
=
0
{\displaystyle x_{CM}={\frac {\int _{-\pi /2}^{+\pi /2}x'dm}{m}}={\frac {\int _{-\pi /2}^{+\pi /2}R\sin \theta {\frac {m}{\pi }}d\theta }{m}}={\frac {R}{\pi }}\left[-\cos \theta \right]_{-\pi /2}^{+\pi /2}=0\ }
come era ovvio per ragioni di simmetria.
Mentre:
y
C
M
=
∫
−
π
/
2
+
π
/
2
y
′
d
m
m
=
∫
−
π
/
2
+
π
/
2
R
cos
θ
m
π
d
θ
m
=
R
π
[
sin
θ
]
−
π
/
2
+
π
/
2
=
2
R
π
{\displaystyle y_{CM}={\frac {\int _{-\pi /2}^{+\pi /2}y'dm}{m}}={\frac {\int _{-\pi /2}^{+\pi /2}R\cos \theta {\frac {m}{\pi }}d\theta }{m}}={\frac {R}{\pi }}\left[\sin \theta \right]_{-\pi /2}^{+\pi /2}={\frac {2R}{\pi }}\ }
→ Vai alla traccia
Scegliamo l'origine e gli assi come in figura.
La densità lineare di massa vale:
λ
=
2
m
π
R
{\displaystyle \lambda ={\frac {2m}{\pi R}}\ }
Mentre l'elemento di lunghezza infinitesima, assunto come variabile l'angolo
θ
{\displaystyle \theta \ }
d
l
=
R
d
θ
{\displaystyle dl=Rd\theta \ }
Quindi:
d
m
=
λ
d
l
=
2
m
π
R
R
d
θ
=
2
m
π
d
θ
{\displaystyle dm=\lambda dl={\frac {2m}{\pi R}}Rd\theta ={\frac {2m}{\pi }}d\theta \ }
Tale generico elemento di trova nel punto di coordinate:
(
x
′
,
y
′
)
=
(
R
sin
θ
,
R
cos
θ
)
{\displaystyle (x',y')=(R\sin \theta ,R\cos \theta )\ }
Quindi:
x
C
M
=
∫
0
π
/
2
x
′
d
m
m
=
∫
0
π
/
2
R
sin
θ
2
m
π
d
θ
m
=
2
R
π
[
−
cos
θ
]
0
π
/
2
=
2
R
π
{\displaystyle x_{CM}={\frac {\int _{0}^{\pi /2}x'dm}{m}}={\frac {\int _{0}^{\pi /2}R\sin \theta {\frac {2m}{\pi }}d\theta }{m}}={\frac {2R}{\pi }}\left[-\cos \theta \right]_{0}^{\pi /2}={\frac {2R}{\pi }}\ }
Che coincide numericamente come si poteva aspettare per ragioni di simmetria con il valore dell'altro asse:
y
C
M
=
∫
0
π
/
2
y
′
d
m
m
=
∫
0
π
/
2
R
cos
θ
2
m
π
d
θ
m
=
2
R
π
[
sin
θ
]
0
π
/
2
=
2
R
π
{\displaystyle y_{CM}={\frac {\int _{0}^{\pi /2}y'dm}{m}}={\frac {\int _{0}^{\pi /2}R\cos \theta {\frac {2m}{\pi }}d\theta }{m}}={\frac {2R}{\pi }}\left[\sin \theta \right]_{0}^{\pi /2}={\frac {2R}{\pi }}\ }
→ Vai alla traccia
a) Mezzo disco
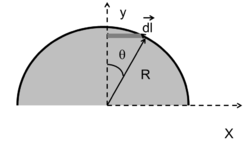
Scegliamo l'origine e gli assi come in figura.
La densità superficiale di massa vale:
σ
=
2
m
π
R
2
{\displaystyle \sigma ={\frac {2m}{\pi R^{2}}}\ }
L'elemento di superficie infinitesimo è alto (larghezza della striscia più scura in figura):
d
h
=
R
d
θ
sin
θ
{\displaystyle dh=Rd\theta \sin \theta \ }
ed ha una lunghezza:
l
=
R
sin
θ
{\displaystyle l=R\sin \theta \ }
L'elemento di superficie infinitesimo dS (striscia più scura in figura) è un rettangolo di superficie:
d
S
=
l
d
h
=
R
2
sin
2
θ
d
θ
{\displaystyle dS=ldh=R^{2}\sin ^{2}\theta d\theta \ }
Quindi:
d
m
=
σ
d
S
=
2
m
π
R
2
R
2
sin
2
θ
d
θ
=
2
m
π
sin
2
θ
d
θ
{\displaystyle dm=\sigma dS={\frac {2m}{\pi R^{2}}}R^{2}\sin ^{2}\theta d\theta ={\frac {2m}{\pi }}\sin ^{2}\theta d\theta \ }
Quindi il generico elemento di superficie si trova ad una quota:
h
=
R
cos
θ
{\displaystyle h=R\cos \theta \ }
Quindi la posizione del centro di massa sull'asse delle y (la coordinata x per simmetria è nulla) vale:
y
C
M
=
∫
−
π
/
2
π
/
2
h
d
m
m
=
∫
−
π
/
2
+
π
/
2
R
cos
θ
2
m
π
sin
2
θ
d
θ
m
=
2
R
π
∫
−
π
/
2
π
/
2
sin
2
θ
(
d
sin
θ
)
=
2
R
π
[
sin
3
θ
3
]
−
π
/
2
+
π
/
2
=
4
R
3
π
{\displaystyle y_{CM}={\frac {\int _{-\pi /2}^{\pi /2}hdm}{m}}={\frac {\int _{-\pi /2}^{+\pi /2}R\cos \theta {\frac {2m}{\pi }}\sin ^{2}\theta d\theta }{m}}={\frac {2R}{\pi }}\int _{-\pi /2}^{\pi /2}\sin ^{2}\theta (d\sin \theta )={\frac {2R}{\pi }}\left[{\frac {\sin ^{3}\theta }{3}}\right]_{-\pi /2}^{+\pi /2}={\frac {4R}{3\pi }}\ }
b) Semisfera
La densità (volumetrica) di massa vale:
ρ
=
3
m
2
π
R
3
{\displaystyle \rho ={\frac {3m}{2\pi R^{3}}}\ }
L'elemento di lunghezza infinitesima, è alto (larghezza del striscia più scura in figura):
d
h
=
R
d
θ
sin
θ
{\displaystyle dh=Rd\theta \sin \theta \ }
L'elemento di volume infinitesimo dV (striscia più scura in figura) è un disco di altezza dh e raggio
r
=
R
sin
θ
{\displaystyle r=R\sin \theta \ }
Quindi:
d
V
=
π
R
3
sin
3
θ
d
θ
{\displaystyle dV=\pi R^{3}\sin ^{3}\theta d\theta \ }
Quindi:
d
m
=
ρ
d
V
=
3
m
2
π
R
3
π
R
3
sin
3
θ
d
θ
=
3
m
2
sin
3
θ
d
θ
{\displaystyle dm=\rho dV={\frac {3m}{2\pi R^{3}}}\pi R^{3}\sin ^{3}\theta d\theta ={\frac {3m}{2}}\sin ^{3}\theta d\theta \ }
Quindi il generico elemento di volume si trova ad una quota:
h
=
R
cos
θ
{\displaystyle h=R\cos \theta \ }
La coordinata y del centro di massa (la x e la z sono nulle per ragioni di simmetria) vale:
y
C
M
=
∫
0
π
/
2
h
d
m
m
=
∫
0
π
/
2
R
cos
θ
3
m
2
sin
3
θ
d
θ
m
=
3
2
R
∫
0
π
/
2
sin
3
θ
(
d
sin
θ
)
=
3
2
R
[
sin
4
θ
4
]
0
π
/
2
=
3
8
R
{\displaystyle y_{CM}={\frac {\int _{0}^{\pi /2}hdm}{m}}={\frac {\int _{0}^{\pi /2}R\cos \theta {\frac {3m}{2}}\sin ^{3}\theta d\theta }{m}}={\frac {3}{2}}R\int _{0}^{\pi /2}\sin ^{3}\theta (d\sin \theta )={\frac {3}{2}}R\left[{\frac {\sin ^{4}\theta }{4}}\right]_{0}^{\pi /2}={\frac {3}{8}}R\ }
→ Vai alla traccia
a) Mezzo disco
Scegliamo l'origine e gli assi come in figura.
La densità superficiale di massa vale:
σ
=
4
m
π
R
2
{\displaystyle \sigma ={\frac {4m}{\pi R^{2}}}\ }
L'elemento di lunghezza infinitesima è alto (larghezza della striscia più scura in figura):
d
h
=
R
d
θ
sin
θ
{\displaystyle dh=Rd\theta \sin \theta \ }
L'elemento di superficie infinitesimo dS (striscia più scura in figura) è un rettangolo di altezza dh e di lunghezza
l
=
R
sin
θ
{\displaystyle l=R\sin \theta \ }
Quindi:
d
S
=
R
2
sin
2
θ
d
θ
{\displaystyle dS=R^{2}\sin ^{2}\theta d\theta \ }
Quindi:
d
m
=
σ
d
S
=
2
m
π
R
2
R
2
sin
θ
d
θ
=
2
m
π
sin
θ
d
θ
{\displaystyle dm=\sigma dS={\frac {2m}{\pi R^{2}}}R^{2}\sin \theta d\theta ={\frac {2m}{\pi }}\sin \theta d\theta \ }
Quindi il generico elemento di superficie si trova ad una quota:
h
=
R
cos
θ
{\displaystyle h=R\cos \theta \ }
Quindi la posizione del centro di massa sull'asse delle y vale:
y
C
M
=
∫
0
π
/
2
h
d
m
m
=
∫
0
π
/
2
R
cos
θ
4
m
π
sin
2
θ
d
θ
m
=
2
R
π
∫
0
π
/
2
sin
2
θ
(
d
sin
θ
)
=
4
R
π
[
sin
3
θ
3
]
0
π
/
2
=
4
R
3
π
{\displaystyle y_{CM}={\frac {\int _{0}^{\pi /2}hdm}{m}}={\frac {\int _{0}^{\pi /2}R\cos \theta {\frac {4m}{\pi }}\sin ^{2}\theta d\theta }{m}}={\frac {2R}{\pi }}\int _{0}^{\pi /2}\sin ^{2}\theta (d\sin \theta )={\frac {4R}{\pi }}\left[{\frac {\sin ^{3}\theta }{3}}\right]_{0}^{\pi /2}={\frac {4R}{3\pi }}\ }
Costruendo un rettangolo verticale invece che orizzontale e ripetendo lo stesso ragionamento si ha che anche:
x
C
M
=
4
R
3
π
{\displaystyle x_{CM}={\frac {4R}{3\pi }}\ }
→ Vai alla traccia
Detto
ρ
{\displaystyle \rho \ }
R
{\displaystyle R\ }
ρ
{\displaystyle \rho \ }
R
/
2
{\displaystyle R/2\ }
R
/
2
{\displaystyle R/2\ }
−
ρ
{\displaystyle -\rho \ }
C
M
{\displaystyle CM\ }
r
C
M
=
−
ρ
4
3
π
(
R
/
2
)
3
R
2
4
3
ρ
π
[
R
3
−
(
R
/
2
)
3
]
=
−
1
14
R
=
−
3.5
c
m
{\displaystyle r_{CM}={\frac {-\rho {\frac {4}{3}}\pi (R/2)^{3}{\frac {R}{2}}}{{\frac {4}{3}}\rho \pi [R^{3}-(R/2)^{3}]}}=-{\frac {1}{14}}R=-3.5\ cm\ }
→ Vai alla traccia
Sul disco agiscono quattro forze la forza peso, la tensione del filo,
la reazione vincolare e la forza esterna.
a)
Scomponiamo la reazione vincolare in una componente normale al piano
R
n
{\displaystyle R_{n}\ }
f
{\displaystyle f\ }
F
+
T
cos
θ
+
f
=
0
{\displaystyle F+T\cos \theta +f=0\ }
Per quanto riguarda i momenti rispetto al baricentro (positivo antiorario):
T
R
sin
θ
−
f
R
=
0
{\displaystyle TR\sin \theta -fR=0\ }
Eliminando
f
{\displaystyle f\ }
T
=
−
F
cos
θ
+
sin
θ
=
−
14.6
N
{\displaystyle T=-{\frac {F}{\cos \theta +\sin \theta }}=-14.6\ N\ }
b)
f
=
T
sin
θ
=
−
7.3
N
{\displaystyle f=T\sin \theta =-7.3\ N\ }
per quanto riguarda la reazione vincolare normale:
R
n
=
−
m
g
−
T
sin
θ
=
37
N
{\displaystyle R_{n}=-mg-T\sin \theta =37\ N\ }
Imponendo che:
|
f
|
≤
μ
s
R
n
{\displaystyle |f|\leq \mu _{s}R_{n}\ }
μ
s
≥
0.2
{\displaystyle \mu _{s}\geq 0.2\ }
c)
Se la forza è applicata in
x
{\displaystyle x\ }
F
+
T
x
cos
θ
+
f
x
=
0
{\displaystyle F+T_{x}\cos \theta +f_{x}=0\ }
Il pedice
T
x
{\displaystyle T_{x}\ }
f
x
{\displaystyle f_{x}\ }
F
{\displaystyle F\ }
x
{\displaystyle x\ }
T
x
R
sin
θ
−
F
(
x
−
R
)
−
f
x
R
=
0
{\displaystyle T_{x}R\sin \theta -F(x-R)-f_{x}R=0\ }
Eliminando
T
x
{\displaystyle T_{x}\ }
f
x
=
F
(
x
−
R
−
R
tan
θ
)
R
(
1
+
t
a
n
θ
)
{\displaystyle f_{x}={\frac {F(x-R-R\tan {\theta })}{R(1+tan{\theta })}}\ }
Che è nulla per
x
−
R
−
R
tan
θ
=
0
{\displaystyle x-R-R\tan {\theta }=0\ }
x
=
0.315
m
=
31.5
c
m
{\displaystyle x=0.315\ m=31.5\ cm\ }
→ Vai alla traccia
a)
La massa della sfera più piccola è:
M
1
=
4
3
π
R
1
3
ρ
F
e
=
0.51
k
g
{\displaystyle M_{1}={\frac {4}{3}}\pi R_{1}^{3}\rho _{Fe}=0.51\ kg\ }
mentre di quella maggiore:
M
2
=
4
3
π
R
2
3
ρ
F
e
=
2.1
k
g
{\displaystyle M_{2}={\frac {4}{3}}\pi R_{2}^{3}\rho _{Fe}=2.1\ kg\ }
Quindi:
M
=
M
1
+
M
2
=
2.6
k
g
{\displaystyle M=M_{1}+M_{2}=2.6\ kg\ }
Il centro di massa del sistema è a destra del fulcro a distanza:
x
C
M
=
−
M
1
ℓ
/
2
+
M
2
ℓ
/
2
M
=
0.03
m
{\displaystyle x_{CM}={\frac {-M_{1}\ell /2+M_{2}\ell /2}{M}}=0.03\ m\ }
b)
Per avere equilibrio il momento delle forze rispetto a
C
{\displaystyle C\ }
T
2
{\displaystyle T_{2}\ }
T
2
ℓ
2
=
M
g
x
C
M
{\displaystyle T_{2}{\frac {\ell }{2}}=Mgx_{CM}\ }
quindi:
T
2
=
M
g
x
C
M
2
ℓ
=
15.5
N
{\displaystyle T_{2}={\frac {Mgx_{CM}2}{\ell }}=15.5\ N\ }
Chiamiamo
T
1
{\displaystyle T_{1}\ }
M
g
=
T
1
+
T
2
{\displaystyle Mg=T_{1}+T_{2}\ }
T
1
=
M
g
−
T
2
=
10
N
{\displaystyle T_{1}=Mg-T_{2}=10\ N\ }
c)
Il momento di inerzia della sfera di sinistra rispetto al fulcro vale:
I
1
=
2
5
M
1
R
1
2
+
M
1
ℓ
2
4
=
0.0014
k
g
m
2
{\displaystyle I_{1}={\frac {2}{5}}M_{1}R_{1}^{2}+M_{1}{\frac {\ell ^{2}}{4}}=0.0014\ kgm^{2}\ }
Il momento di inerzia della sfera di destra rispetto al fulcro vale:
I
2
=
2
5
M
2
R
2
2
+
M
2
ℓ
2
4
=
0.0066
k
g
m
2
{\displaystyle I_{2}={\frac {2}{5}}M_{2}R_{2}^{2}+M_{2}{\frac {\ell ^{2}}{4}}=0.0066\ kgm^{2}\ }
Quindi il momento di inerzia totale vale:
I
=
I
1
+
I
2
=
0.008
k
g
m
2
{\displaystyle I=I_{1}+I_{2}=0.008\ kgm^{2}\ }
Quando si spezza il filo dalla seconda equazione cardinale:
I
α
=
M
g
x
C
M
{\displaystyle I\alpha =Mgx_{CM}\ }
α
=
M
g
x
C
M
I
=
97
r
a
d
/
s
2
{\displaystyle \alpha ={\frac {Mgx_{CM}}{I}}=97\ rad/s^{2}\ }
d)
Nel punto più basso l'energia potenziale del sistema è diventata cinetica:
1
2
I
ω
2
=
M
g
x
C
M
{\displaystyle {\frac {1}{2}}I\omega ^{2}=Mgx_{CM}\ }
ω
=
2
M
g
x
C
M
I
=
13.9
r
a
d
/
s
{\displaystyle \omega ={\sqrt {\frac {2Mgx_{CM}}{I}}}=13.9\ rad/s\ }



























































![{\displaystyle x_{CM}={\frac {\int _{-\pi /2}^{+\pi /2}x'dm}{m}}={\frac {\int _{-\pi /2}^{+\pi /2}R\sin \theta {\frac {m}{\pi }}d\theta }{m}}={\frac {R}{\pi }}\left[-\cos \theta \right]_{-\pi /2}^{+\pi /2}=0\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/341702964f801b87cbf0f7fa57e07c5f83844ea8)
![{\displaystyle y_{CM}={\frac {\int _{-\pi /2}^{+\pi /2}y'dm}{m}}={\frac {\int _{-\pi /2}^{+\pi /2}R\cos \theta {\frac {m}{\pi }}d\theta }{m}}={\frac {R}{\pi }}\left[\sin \theta \right]_{-\pi /2}^{+\pi /2}={\frac {2R}{\pi }}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/763393d19d8721a19bdb50a30c234a994695a0f1)


![{\displaystyle x_{CM}={\frac {\int _{0}^{\pi /2}x'dm}{m}}={\frac {\int _{0}^{\pi /2}R\sin \theta {\frac {2m}{\pi }}d\theta }{m}}={\frac {2R}{\pi }}\left[-\cos \theta \right]_{0}^{\pi /2}={\frac {2R}{\pi }}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/67ffb514a2bc999bea69a9a02336c2a5b445b91b)
![{\displaystyle y_{CM}={\frac {\int _{0}^{\pi /2}y'dm}{m}}={\frac {\int _{0}^{\pi /2}R\cos \theta {\frac {2m}{\pi }}d\theta }{m}}={\frac {2R}{\pi }}\left[\sin \theta \right]_{0}^{\pi /2}={\frac {2R}{\pi }}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6e0da000da504a6452f52ea93bcac2d4f73ba42)






![{\displaystyle y_{CM}={\frac {\int _{-\pi /2}^{\pi /2}hdm}{m}}={\frac {\int _{-\pi /2}^{+\pi /2}R\cos \theta {\frac {2m}{\pi }}\sin ^{2}\theta d\theta }{m}}={\frac {2R}{\pi }}\int _{-\pi /2}^{\pi /2}\sin ^{2}\theta (d\sin \theta )={\frac {2R}{\pi }}\left[{\frac {\sin ^{3}\theta }{3}}\right]_{-\pi /2}^{+\pi /2}={\frac {4R}{3\pi }}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9447080e2a05d66482aa266439c438d0caef0492)




![{\displaystyle y_{CM}={\frac {\int _{0}^{\pi /2}hdm}{m}}={\frac {\int _{0}^{\pi /2}R\cos \theta {\frac {3m}{2}}\sin ^{3}\theta d\theta }{m}}={\frac {3}{2}}R\int _{0}^{\pi /2}\sin ^{3}\theta (d\sin \theta )={\frac {3}{2}}R\left[{\frac {\sin ^{4}\theta }{4}}\right]_{0}^{\pi /2}={\frac {3}{8}}R\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2a2dbeb3056c9d5db2fc498ab6cd5356de1a346)



![{\displaystyle y_{CM}={\frac {\int _{0}^{\pi /2}hdm}{m}}={\frac {\int _{0}^{\pi /2}R\cos \theta {\frac {4m}{\pi }}\sin ^{2}\theta d\theta }{m}}={\frac {2R}{\pi }}\int _{0}^{\pi /2}\sin ^{2}\theta (d\sin \theta )={\frac {4R}{\pi }}\left[{\frac {\sin ^{3}\theta }{3}}\right]_{0}^{\pi /2}={\frac {4R}{3\pi }}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/94012d75615903ae864598cbfcfd78b1bf698f25)




![{\displaystyle r_{CM}={\frac {-\rho {\frac {4}{3}}\pi (R/2)^{3}{\frac {R}{2}}}{{\frac {4}{3}}\rho \pi [R^{3}-(R/2)^{3}]}}=-{\frac {1}{14}}R=-3.5\ cm\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e0387ad1556ab1017372d3b0edcc098a0391df6)

































