Variabili probabilistiche nella conduzione operativa del sonar

Processo di conduzione operativa di un sonar

Video da P.C. con segnali e rumori in assenza di soglia di rivelazione

 

Video da P.C con soglia di rivelazione (zona oscurata)

Nei calcoli della portata di scoperta sonar sono sistematicamente introdotti il valore del $DT$ (Soglia di rivelazione nella scoperta sonar) scegliendo, in base ai diversi esempi da svolgere, la larghezza di banda di ricezione $BW$, la costante d'integrazione $RC$ ed infine il valore $d$ legato ad una coppia di valori relativi alla probabilità di falso allarme $Pfa$ e di scoperta $Priv$; tali scelte sono fatte senza approfondire il criterio d'impostazione del $DT$, da parte dell'operatore, non valutando le conseguenze che queste provochino sulle caratteristiche delle portate di scoperta.

In questa voce alcuni esempi dei processi operativi che sono messi in atto nella conduzione del sonar, con l'impiego della soglia di rivelazione, nelle fasi di sorveglianza e/o attacco del sottomarino.

Sul tipo di rivelazione e le sue formule

Schema a blocchi di un correlatore a coincidenza dipolarità

Per lo svolgimento degli esempi citati è necessario fissare alcuni punti sui sistemi di rivelazione dei segnali nel sonar e sulle formule di calcolo che li definiscono:

• Le formule illustrate sono relative a sistemi di rivelazione dei segnali in correlazione del tipo a coincidenza di polarità

• Le formule sono valide per piccoli rapporti segnale/disturbo indicati come: $Si/Ni$ (misurati all'ingresso dei correlatori)

• Le variabili, banda di ricezione e costante di tempo d'integrazione, sono riferite a $BW\ in\ Hz$ (banda dei segnali da correlare) $RC\ in\ s.$(costante di tempo d'integrazione dei correlatori)

• Per le variabili $BW\ e\ RC$di cui al punto terzo, pur nella disponibilità dell'operatore, non sono previste variazioni nell'analisi del I caso della seconda sezione.

• La formula che esprime il $DT$ (soglia di rivelazione) è espressa come segue:

$DT=5\ \log \ [d\ BW/(2\ RC)]$

La variabile $d$ di cui al punto precedente è dipendente da $Si/Ni$ secondo l'espressione: $d=2\ BW\ RC\ (Si/Ni)^{4}$

• Dalla variabile $d$ di cui al punto precedente dipendono innumerevoli coppie di valori statistici quali:

$Pfa\$ ( probabilità percentuale di falso allarme), $Priv\$(probabilità percentuale di rivelazione)

• Essendo $d$ funzione di $Si/Ni$ anche per tale rapporto dipendono, secondo le curve ROC (vedi sezione seguente):

$Pfa\$ ( probabilità percentuale di falso allarme), $Priv\$(probabilità percentuale di rivelazione)

Esposizione delle curve ROC

Curve ROC

Diagramma per l'impiego delle curve ROC :

• In ascisse la probabilità di falso allarme $Pfa$ in %
• In ordinate la probabilità di rivelazione $Priv$ in %
• Nel tracciato serie di $7$ curve parametriche secondo $d\$ da $0$ a $36$

due esempi:

Per $Priv=50\%\ e\ Pfa=0.2\%$ si ha $d=9$

Per $Priv=50\%\ e\ Pfa=2\%$ si ha $d=4$

Esempi per il calcolo di previsione di portata del sonar

I caso

Sono riportate di seguito, per un'analisi approfondita, le parti essenziali di un esempio riguardante soltanto le procedure di calcolo.

Si supponga che l'operatore esegua il calcolo di previsione della portata del sonar secondo le caratteristiche dell'apparato e sulla base delle condizioni esterne.

Valori delle variabili del sonar

$F_{1}\ ;\ F_{2}\$ estremi di banda delle frequenze di ricezione: $F_{1}=1000\ Hz\ ;\ F_{2}=3000\ Hz$

$f_{o}\$ frequenza media geometrica nella banda: $f_{o}=1.7\ kHz$

$DI\$ guadagno di direttività della base ricevente: $DI=10\ dB$

$RC$ costante di tempo d'integrazione: $RC=0.1\ s$

$BW\$ larghezza di banda del ricevitore: $BW=F_{2}\ -\ F_{1}=2000\ Hz$

Valori assunti dall'operatore

L'operatore vuole eseguire la ricerca del bersaglio con la probabilità di scoperta $Priv=90\%\$ accettando un falso allarme $Pfa=5\%$.

Questa coppia di variabili probabilistiche è individuata sulle curve ROC per $d=9$, valore con il quale si calcola la soglia di rivelazione $DT$ nella scoperta sonar .

$DT=5\ \log \ [d\ BW/(2\ RC)]=5\ \log \ [9\cdot 2000/(2\cdot 0.1)]\approx 25\ dB$

Valori delle variabili dell'ambiente

• Propagazione: tipo sferica

• $SL$ sorgente del segnale: cacciatorpediniere di vecchia generazione

che naviga a $20$ nodi; dai tabulati in letteratura, per $f_{o}=1.7\ kHz$ , si ha $SL=140\ dB/\mu \ Pa/Hz$

• $NL$ forza del mare per $SS=2$ ; dai tabulati in letteratura, per

$fo=1.7\ kHz,$ si ha $NL=58\ dB/\mu \ Pa/Hz$

• $\alpha$ Attenuazione per assorbimento secondo la legge di W H Thorp:

$\alpha =\left[{\frac {0.1\cdot fo^{2}}{1+fo^{2}}}\right]+\left[{\frac {40\cdot fo^{2}}{4100+fo^{2}}}\right]+\left[{\frac {2.75\cdot fo^{2}}{10^{4}}}\right]$

dove $\alpha \ in\ dB/km$ e $fo\ in\ kHz$; per $fo=1.7\ kHz$ si ha $\alpha =0.1\ dB/km$

Equazioni del sonar passivo

• b1) $TL=SL+DI-NL-DT+10\cdot \log BW=$

$=140\ dB+10\ dB-58\ dB-25\ dB+10\cdot \log 2000=100\ dB$

Dopo il calcolo in b1) si computa ora la variazione del $TL$ in funzione della distanza $R$ e del coefficiente di assorbimento $\alpha$:

• b2) $TL=60\ dB+20\cdot \log \ R+\alpha R=$

$60\ dB+20\log \ R+0.1\ R$

Determinazione grafica della portata di scoperta

Tracciata , su carta millimetrata, la curva di $TL$ secondo la b2) e la retta $TL$ secondo la b1) in un sistema di assi cartesiani dove, posto $R$ in ascisse e $TL$ in ordinate, si ottiene il grafico riportato:

Grafico risolutivo della portata di scoperta

Dal punto d'intersezione tra le due curve si ricava il valore $R\approx 56\ Km.$

Esame del risultato

Il valore di $R$ ottenuto dalla procedura numerico-grafica rappresenta la previsione della massima distanza di scoperta del bersaglio secondo le variabili generali ipotizzate per il sonar e la scelta fatta dall'operatore con l'intenzione d'impostare, in fase di operatività sul campo, specifiche condizioni di rivelazione: $Priv=90\%\ Pfa=5\%$.

II caso

Il primo caso vede la scelta di $Pfa=5\%$ fatta dall'operatore con l'intenzione d'impostare, in fase di scoperta sul campo, la soglia di rivelazione $DT=25\ dB$ affinché tale percentuale di falsi allarmi si verifichi, lasciando poi alle dimensioni delle altre variabili il concretizzarsi di un rapporto $Si/Ni$ tale da consentire una probabilità di scoperta $Priv$ del $90\%.$

Se l'operatore, a parità del valore $DT=25\ dB$, varia il livello di soglia accettando ad esempio un $Pfa=10\%$ la portata resta inalterata per $R\approx 56\ km$ ma, secondo le curve ROC, la probabilità di scoperta $Priv$ cresce dal $90\%\ al\ 96\%.$

III caso

Se l'operatore, sempre a parità del valore $DT$, decide di ottenere una probabilità di falso allarme $Pfa=1\%$ la portata resta inalterata per $R\approx 56\ km$ ma, secondo le curve ROC, la probabilità di scoperta $Priv$ decresce dal $90\%\ al\ 75\%.$

Ne segue che l'operatore, in base alle condizioni sul campo, decide quale soglia di rivelazione impostare per ottimizzare la scoperta del bersaglio.

Nelle condizioni esaminate si può calcolare il rapporto $S_{i}/N_{i}$ all'ingresso del sistema di rivelazione secondo l'espressione che utilizza i dati esposti nel primo caso:

IV Caso

Se si desidera ottenere un miglioramento delle condizioni di scoperta riducendo la probabilità di falso allarme $Pfa$ e contemporaneamente ottenere un incremento della probabilità di rivelazione $Priv$ si deve agire sul $DT$ al fine di migliorare il rapporto $S_{i}/N_{i}$.

In questo caso si può calcolare il rapporto $S_{i}/N_{i}$ all'ingresso del sistema di rivelazione secondo l'espressione che utilizza, ad esempio, i dati esposti nel primo caso:

$S_{i}/N_{i}=20\ \log \ \ [$ $_{4}{\sqrt {d/(2\ Bw\ RC)}}\ \ ]=-8.2\ dB$

L'operatore può impostare un nuovo calcolo di previsione della portata al fine di osservare, dal solo punto di vista numerico, le condizioni di scoperta rispetto al I caso esaminato in precedenza, utilizzando le stesse variabili impiegate salvo il valore del $DT$che deve aggiornare per ottenere, ad esempio, $Pfa=1\%\ e\ Priv=99\%.$

Dalle curve ROC si vede che una tale coppia di valori fa parte delle innumerevoli altre coppie relative ad un valore $d=21$; il nuovo valore del $DT\ per\ d=21$ è $DT=5\ \log \ [d\ BW/(2\ RC)]=26.6\ dB$

Seguendo le sviluppo del calcolo eseguito nel I caso si ha: $R\approx 49\ km$ con valore di $Si/Ni=-6.4\ dB.$

L'operatore quindi, ponendo la soglia per accettare una $Pfa=1\ \%,$ prevede la rivelazione del bersaglio alla distanza di $49\ km$ con una probabilità di scoperta di $Priv=99\%$.

Se la soglia viene regolata per un $Pfa=0.1\%$ la probabilità di scoperta, secondo le curve ROC, scende da $Priv=99\%\ a\ Priv=94\%$restando invariata la distanza di scoperta $R=49\ km$.

L'operatore ha ottenuto, sulla carta, il miglioramento delle condizioni di scoperta pagando con una riduzione della distanza che è scesa da $R\approx 56\ km\ a\ R\approx 49\ km.$

Osservazioni

Se confrontiamo i dati calcolati nel I caso con quelli elaborati di seguito vediamo che a parità di variabili, salvo il valore del $DT,$ i risultati sono diversi pur restando le caratteristiche peculiari del sonar e le condizioni ambientali le stesse.

La variazione del valore del $DT,$ a seguito del cambiamento del $d\$ da $d=9\$ a $d=21$, indica diverse possibilità di scoperta del bersaglio quando questo è più vicino che nel caso precedente.

Infatti quando l'operatore, dopo aver eseguito i calcolo di previsione portata, si accinge alla reale scoperta del bersaglio, indipendentemente dal valore di $R$ calcolato, può trovarsi con bersagli a distanze inferiori ad $R,$ in tal caso potrà regolare la soglia per ridurre la probabilità di falso allarme ottenendo migliori probabilità di scoperta, oppure può trovare bersagli a distanza superiore ad $R$ che, se possibile, consentiranno la scoperta con un falso allarme più elevato del precedente.

Simulazione di operazione sul campo

Curva $S_{i}\ /\ N_{i}$ funzione della distanza $R$

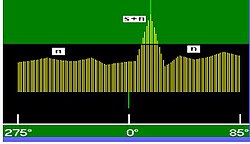
Il processo che segue, diverso dalla scoperta del bersaglio, consiste nella simulazione di un controllo, con bersaglio certamente presente, per l'impostazione della soglia e la determinazione della probabilità di scoperta conseguente. Per meglio comprendere come giocano le variabili probabilistiche, $Pfa\ e\ Priv$, nella scoperta sonar è utile una simulazione di attività sul campo che si avvale del diagramma, $S_{i}\ /\ N_{i}$ funzione della distanza $R$ , nel quale è tracciata una curva che mostra come varia il rapporto $S_{i}/N_{i}$, all'ingresso del rivelatore, in funzione della distanza $R.$

La curva, ottenuta dall'elaborazione delle equazioni b1) e b2) del I caso , mostra come varia $S_{i}/N_{i}$ con il variare della distanza $R$ del bersaglio; quando la distanza aumenta si riduce l'intensità $S_{i}$ del segnale ricevuto e peggiora quindi il rapporto $S_{i}/N_{i}.$

La curva è tracciata per un sonar passivo ed un ambiente perfettamente identici a quelli esaminati nel I caso con il bersaglio, all'inizio della simulazione, alla distanza di $46\ km.$

Nella situazione iniziale, bersaglio a $46\ km$ curva mostra un rapporto $S_{i}/N_{i}=-6\ dB$ al quale corrisponde, secondo la formula di paragrafo 2):

$d=2\ BW\ RC\ (S_{i}/N_{i})^{4}=2\ (2000)\ (0.1)\ (0.5)^{4}=25$ .

Se l'operatore imposta la soglia per accettare una probabilità di falso allarme

$=0.1\ \%,$ essendo $d=25$, avrà una probabilità di scoperta $Priv=97.67\%$ (vedi curve ROC )

Dopo il primo rilievo il bersaglio si allontana e si porta ad una distanza di $50\ km$, alla quale, secondo la curva si ha $S_{i}/N_{i}=-7\ dB$ al quale corrisponde:

$d=2\ (2000)\ (0.1)\ (0.45)^{4}=16.$

Se l'operatore lascia invariata la soglia per $Pfa=0.1\%$ la probabilità di scoprire il bersaglio scende da $Priv=97.67\%\ a\ Priv=83.89.$(vedi curve ROC)

Il bersaglio si porta ora a $60\ km$, a questa distanza risulta $Si/Ni=-10\ dB$ e il valore di $d$ scende a:

$d=2(2000)(0.1)(0.31)^{4}=3.7.$

Se l'operatore lascia ancora invariata la soglia per $Pfa=0.1\%$ la probabilità di scoprire il bersaglio scende a $Priv=13.86\%$(vedi curve ROC) è chiaro a questo punto che l'operatore deve modificare la soglia per aumentare la probabilità di scoperta che altrimenti è irrilevante.

Variando la soglia per $Pfa=1\%$ si ha $Priv=34.22\%$ (vedi curve ROC).

Se l'operatore ritiene tale valore ancora troppo basso può impostare la soglia per $Pfa=10\%$ ottenendo $Priv=73.78\%.$

La simulazione del bersaglio in allontanamento può proseguire per distanze superiori a $60\ km$; la procedura di calcolo resta quella ora mostrata.

Bibliografia

• WH Thorp,, "Analytical description of the low frequency attenuation coefficient", Acoustical Society of America Journal, vol. 42, 1967, pag. 270..

• G. Pazienza, Fondamenti della localizzazione marina, Studio grafico Restani, 1970.

• (EN) Robert J. Urick, Principles of underwater sound, 3ª ed., Mc Graw – Hill, 1968.

• C. Del Turco, La correlazione, La Spezia, Edizioni scientifiche Moderna, 1968.

• Del Turco, Sonar-principi-tecnologie-applicazioni, La Spezia, Edizioni scientifiche Moderna, 1968.

Collegamenti esterni

N° FASCI Selenia

Sonar FALCON

Schemi sonar FALCON

Testo discorsivo sul sonar

Testo tecnico sulla Correlazione