Richiami di Insiemistica

Un insieme è un contesto in cui vengono raggruppati degli elementi aventi una o più caratteristiche in comune (ad esempio, il contesto in cui è contenuto l'elemento "piccione" assieme ad altri volatili sarà l'insieme degli uccelli).
Essi solitamente si indicano con le lettere maiuscole, mentre gli elementi che fanno parte di un insieme si indicano con le lettere minuscole.
Chiamiamo per esempio insieme C l'insieme contenente tutti i corvidi, comprendente quindi il corvo a, la cornacchia b, la ghiandaia c ecc.
Gli elementi a, b e c appartengono all'insieme C perché in comune hanno la caratteristica di appartenere alla famiglia dei corvidi.
Introduzione
[modifica]Si scrive quando l'elemento a fa parte dell'insieme A (letto correttamente: a appartiene all'insieme A), mentre significa che l'elemento a non appartiene all'insieme A.
Dall'esempio precedente, perché la taccola è un corvide, mentre perché l'anguilla è un pesce.
Generalmente, l'insieme si descrive esplicitando gli elementi in esso contenuti, elencandoli tra parentesi graffe:
L'insieme A è composto dagli elementi {1, 2, 3, 4}.
Questa rappresentazione è detta rappresentazione per elencazione o rappresentazione tabulare.
E' anche possibile descrivere un insieme di elementi finiti raffigurandolo come una curva chiusa, i cui elementi sono rappresentati all'interno come dei punti. Questa viene detta rappresentazione grafica.
Questo metodo di rappresentazione degli insiemi (come spazi chiusi contenenti gli elementi rappresentati come punti) è detto diagrammi di Eulero-Venn.
Gli insiemi si possono anche rappresentare attraverso una formula matematica che generalizzi tutti gli elementi in esso contenuti: questo tipo di rappresentazione è detta rappresentazione mediante la proprietà caratteristica.
Per esempio, l'insieme D contiene tutti i numeri dispari (D = {1, 3, 5, ...}). Non è necessario (né realmente possibile) elencare uno alla volta ognuno dei membri che lo costituiscono; ci limiteremo quindi ad enunciarne la proprietà caratteristica che li accomuna, ossia essere dispari:
(La formula si legge è l'insieme di elementi chiamati i quali appartengono all'insieme dei numeri naturali () e sono dispari.)
Insiemi molto importanti per la nostra materia sono gli insiemi numerici contenenti rispettivamente: tutti i numeri naturali, tutti i numeri relativi, tutti i numeri razionali, tutti i numeri reali e tutti i numeri complessi.
Questi insiemi descrivono la totalità dei numeri, e verranno ampiamente usati nello studio di logica ed insiemistica.
Un insieme particolare è l'insieme vuoto che si indica con il simbolo : esso indica un insieme privo di alcun elemento, e come tale è sottoinsieme di tutti gli insiemi. Un altro insieme particolare è l'insieme universo. Questo, indicato con il simbolo comprende tutti gli oggetti della classe di insiemi di cui si sta parlando. Per esempio se si parla di insiemi di lettere, l'Universo conterrà l'alfabeto. Quando si usano insiemi numerici l'Universo sarà l'insieme dei numeri.

I sottoinsiemi dell'insieme possono essere disposti in maniera differente: l'uno vicino all'altro, alcuni intersecati fra loro, altri totalmente inglobati l'uno nell'altro (come una matriosca).
Tra gli insiemi numerici vigono le seguenti inclusioni:
- .
Il simbolo indica che tutti gli elementi di A sono inclusi nell'insieme B e si dice che A è un sottoinsieme di B oppure che A è incluso in B.
Per esempio gli insiemi e sono entrambi sottoinsiemi di .
Il simbolo ammette che i due insiemi siano uguali, (es ) mentre il simbolo detto anche "sottoinsieme stretto" non ammette che i due insiemi siano uguali.
A volte per sottolineare la negazione dell'uguaglianza viene usato anche il simbolo .
Se A è un insieme che ha un numero finito di elementi, allora si utilizzerà il simbolo . Per indicare il numero degli elementi che contiene si usa il fattore detto cardinalità.
La cardinalità di un insieme è il numero di elementi in esso contenuti.
Ad esempio nell'insieme A = {0, 1, 2} la cardinalità è 3 (letto correttamente: l'insieme A ha cardinalità 3).
Operazioni tra insiemi
[modifica]


Quando due o più insiemi si uniscono, perché hanno elementi in comune fra di loro, viene a crearsi un complesso di insiemi, le cui parti possono essere considerate singolarmente, (considero solo gli elementi in comune, considero solo gli elementi non ecc.) e definibili tramite un particolare tipo di scrittura matematica:
- Unione di insiemi: è un terzo insieme costituito da tutti gli elementi di A e di B (comuni e non comuni), senza ripeterli.
(Si legge: A unito B è l'insieme comprendente quegli elementi -detti x- i quali appartengono ad A o a B).
- Intersezione di insiemi: è un terzo insieme costituito solo dagli elementi comuni sia ad A che a B.
(Si legge: Intersezione di A con B è l'insieme comprendente quegli elementi -detti x- i quali appartengono sia ad A che B, esclusi dunque quelli appartenenti solo ad A e solo a B).
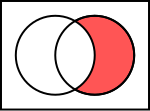
- Differenza di insiemi: è un terzo insieme costituito dagli elementi di B che non fanno parte di A (vanno tolti anche quelli in comune):
(Si legge: Intersezione di A con B è l'insieme comprendente quegli elementi -detti x- i quali appartengono solo a B e non ad A, escludendo anche l'intersezione).
- Differenza simmetrica: è l'insieme degli elementi che appartengono ad A e non a B oppure che appartengono a B e non ad A.
- Prodotto cartesiano di insiemi è costituito da tutte le coppie ordinate create accoppiando ogni elemento di A con ogni elemento di B, scritto e :
(Si crea semplicemente associando, uno per volta, ad ogni termine di A ognuno dei termini di B, senza mai ripetere la stessa coppia).
Proprietà degli insiemi
[modifica]Per gli insiemi valgono:
- Proprietà commutativa dell'unione e dell'intersezione:
- Proprietà associativa dell'unione e dell'intersezione:
- Proprietà riflessiva dell'unione e dell'intersezione:
- Proprietà distributiva:
- .
Si noti che la differenza è anti-commutativa.
Particolarità
[modifica]L'insieme vuoto è l'elemento neutro dell'unione:
L'insieme universo è l'elemento neutro dell'intersezione:
Unendo un insieme con l'universo si ottiene l'universo stesso:
Intersecando un insieme con l'insieme vuoto, si ottiene un altro insieme vuoto:
Si definisce complemento di un insieme ad un altro insieme, un terzo insieme che sommato al primo dà il secondo. Facendo la differenza tra l'universo ed un dato insieme A, si ottiene il complemento di A all'universo. Questo vale solo nel caso in cui il secondo insieme è sottoinsieme del primo:


















































