Misura della quota di un bersaglio sonar

Questa voce è dedicata ad un argomento poco conosciuto; la misura della quota dei bersagli sonar e degli errori generati dalla propagazione anomala.

La misura della quota interessa, prevalentemente, le azioni operative di attacco nelle quali la distanza del bersaglio è contenuta in alcune migliaia di metri.

Il processo del misuratore di quota

figura 1: geometria per la misura della quota del bersaglio

La misura della quota di un bersaglio è affidata al rilevamento, nel piano verticale, delle variabili $R\ e\ \beta$ ; così come mostra la figura 1:

La quota $Hqv$ (virtuale) è calcolata in funzione di $R\ e\ \beta$ ; secondo le espressioni:

$Hqv=R\cdot \operatorname {sen} \beta \ \ \$ 1)

oppure:

$Hqv=Ro\cdot \tan \beta \ \ \$ 2)

valida soltanto in condizioni di propagazione ideale ^[1]; le due variabili $R\ e\ \beta$ possono essere rilevate come segue:

La distanza $R$ può essere calcolata, o con il metodo dell'eco o con un misuratore passivo della distanza.

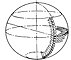
L'angolo $\beta$ può essere rilevato da un sistema a fasci preformati collegato ad una base sferica, vedi figura 2; con i fasci che si sviluppano nel piano verticale:

Sottomarino con base sferica (non in scala)
Figura 2: Base sferica

Propagazione anomala del suono

Una curva di propagazione anomala del suono è mostrata in figura 3 ^[2]:

Le variabili utilizzate nel grafico sono espresse con unità di misura anglosassoni:

Temperature: (°F ) in gradi Fahrenheit ( °F = °C x 9/5 + 32)

Profondità: (ft) in feet ( ft = mt x 3.281 )

Distanze: (yd) in yard (yd = m x 1.094 )

Nella parte di sinistra è mostrato un batitermogramma tipico nel quale si ha temperatura costante da quota $0$ a quota $64\ ft$ e temperatura decrescente in modo lineare da $64\ ft$ in poi; come è noto a questo corrisponde il diagramma relativo alla velocità del suono (il bativelocigramma).

Nel diagramma di destra è tracciato un raggio acustico che si propaga dall'origine fino ad una distanza $Ro\approx 2800\ yd$ ; nel tratto compreso tra la sorgente e quota $64\ ft$ il raggio curva leggermente dato il modesto gradiente della velocità del suono dovuto alla pressione, sotto quota $64\ ft$ il raggio piega vistosamente a causa del sensibile gradiente della velocità del suono a seguito della variazione di temperatura per le quote oltre i $64\ ft.$

Nel calcolo della curva l'angolo di radenza del primo tratto del raggio è di $0.012$ rad.

Valutazione della quota secondo la propagazione anomala

figura 4: Valutazioni sulla curva di propagazione anomala del suono

Se sulla curva di figura 3 ipotizziamo ad esempio un bersaglio alla distanza $Ro=2200\ yd$ visto sotto un angolo $\beta =0.012\ rad$ possiamo valutare a quale profondità reale si rileva il bersaglio; dall'esame della figura 4 risulta che alla distanza di $2200\ yd$ la quota del bersaglio è di $Hq=120\ ft$

Queste considerazioni sono state possibili grazie all'osservazione del tracciato della curva computato a priori.

Valutazione della quota secondo la propagazione ideale

Supponiamo ora di non disporre della curva di figura 4 e che, durante un rilievo fisico indirizzato ala misura della quota di un bersaglio, si siano misurati con il sonar sia l'angolo $\beta =0.012\ rad$ , sia la distanza $Ro=2200\ yd$ , in tal caso la quota virtuale è calcolabile soltanto con la 2):

$Hqv=2200\cdot \tan(0.012\ rad)=26.4\ yd=79.2\ ft.$

Se tracciamo quest'ordinata nel diagramma di figura 4, all'ascissa $Ro=2200\ yd$ , e la congiungiamo con l'origine abbiamo la figura 5 nella quale si confronta il percorso di un raggio acustico in ambiente ideale a velocità del suono costante con un raggio in ambiente anomalo che parte con lo stesso angolo di radenza $\beta$ .

Dalla figura si vede la differenza tra la quota virtuale $Hqv$ pari a $79.2\ ft$ , ottenuta dal calcolo, e la quota reale $Hq$ di $120\ ft$ dovuta al percorso anomalo del raggio; questo esempio mostra un errore di quota di $\approx -39\%$ rispetto alla quota reale.

Diverso sarebbe il caso in cui con $\beta =0.012\ rad$ fosse $Ro=1800\ yd$ :

Secondo la 2) si avrebbe :

quota virtuale: $Hqv=1800\ yd\ \cdot \tan(0.012\ rad)=21.26\ yd=63.78\ ft.$

e secondo il grafico di figura 4 : quota reale: $\ Hq=50\ ft$

in questo caso l'errore sarebbe positivo: $\approx +27\%$ rispetto alla quota reale.

note

↑ Si ha propagazione ideale quando le onde acustiche si propagano secondo i raggi di una sfera od un cilindro; generalmente la propagazione del suono in mare non è tale e si definisce come anomala.
↑ Il grafico, avendo le ascisse in yd e le ordinate in ft è deformato; ciò allo scopo di poter visualizzare ampiezze dell'angolo di radenza moto piccole, ad esempio $\beta =0.012\ rad$ .

Bibliografia

G. Pazienza, Fondamenti della localizzazione marina, Studio grafico Restani, La spezia, 1970.

Cesare Del Turco, Sonar- Principi - Tecnologie – Applicazioni , Tip. Moderna La Spezia, 1992

·

[1] Si ha propagazione ideale quando le onde acustiche si propagano secondo i raggi di una sfera od un cilindro; generalmente la propagazione del suono in mare non è tale e si definisce come anomala.

[2] Il grafico, avendo le ascisse in yd e le ordinate in ft è deformato; ciò allo scopo di poter visualizzare ampiezze dell'angolo di radenza moto piccole, ad esempio $\beta =0.012\ rad$ .

[1]

[2]