Figure uguali: le isometrie (scuola media)

Quali sono le proprietà geometriche di uno specchio?
Cominciamo con lo studio delle trasformazioni geometriche che permettono di riprodurre una copia di una figura piana.
Queste trasformazioni devono per evidenti motivi mantenere le misure delle figure copiate e prendono quindi il nome di isometrie, dal greco uguale misura.
Simmetria assiale
[modifica]
La simmetria assiale è la trasformazione che si ottiene rispecchiando la figura aldilà di una retta.
I punti dell'immagine giacciono sulla retta perpendicolare all'asse di simmetria alla stessa distanza dei punti della figura originale.
Simmetria assiale nel piano cartesiano
[modifica]In generale date le coordinate di un punto e l'equazione dell'asse di simmetria esiste una formula che permette di ricavare le coordinate del punto simmetrico.
Riportiamo qui alcuni casi particolari che permettono di comprendere la relazione tra le coordinate di un punto e della sua immagine simmetrica.
Simmetria assiale rispetto all'asse y
[modifica]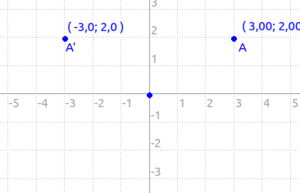
Nel piano cartesiano la simmetria assiale rispetto all'asse Y fa si che dalle coordinate del punto A (x,y) si ricavano facilmente le coordinate del suo punto simmetrico A' (-x,y).
Simmetria assiale rispetto all'asse x
[modifica]
Nel piano cartesiano la simmetria assiale rispetto all'asse X fa si che dalle coordinate del punto A (x,y) si ricavano facilmente le coordinate del suo punto simmetrico A' (x,-y).
Simmetria assiale rispetto alla bisettrice I e III quadrante
[modifica]
Nel piano cartesiano la simmetria assiale rispetto alla bisettrice del I e del III quadrante fa si che dalle coordinate del punto A (x,y) si ricavano facilmente le coordinate del suo punto simmetrico A' (y,x).
Simmetria assiale rispetto alla bisettrice II e IV quadrante
[modifica]
Nel piano cartesiano la simmetria assiale rispetto alla bisettrice del II e del IV quadrante fa si che dalle coordinate del punto A (x,y) si ricavano facilmente le coordinate del suo punto simmetrico A' (-y,-x).
Simmetria centrale
[modifica]Come per la simmetria assiale in generale date le coordinate di un punto e quelle del centro di simmetria esiste una formula che permette di ricavare le coordinate del punto simmetrico.
Riportiamo qui alcuni il caso particolare della simmetria centrale rispetto all'origine degli assi, cosa che permetto di comprendere facilmente la relazione tra le coordinate di un punto e della sua immagine simmetrica.
Simmetria centrale rispetto all'origine
[modifica]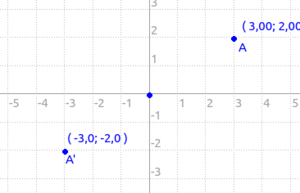
Nel piano cartesiano la simmetria centrale rispetto all'origine fa si che dalle coordinate del punto A (x,y) si ricavano facilmente le coordinate del suo punto simmetrico A' (-x,-y).
Simmetrie su scratch (coding)
[modifica]Simmetrie su geogebra
[modifica]Traslazione
[modifica]

