Divisibilità e fattorizzazione: mcm e MCD (scuola media)

Mappa della lezione per chi vuole leggere poco

Si può fruire di questa lezione in forma di mappa mentale su wiki2map

Divisioni e divisioni con il resto

La divisione nei numeri naturali genera un solo risultato solo se il dividendo è divisibile per il divisore, altrimenti, la divisione ci restituisce un quoziente ed un resto come nell'esempio qui sotto dove il quoziente è $41$ ed il resto è $15$:

${\begin{aligned}&{\widehat {75}}{\breve {3}}:18=41\\&{\underline {72\ \ \ }}\\&\ \ 33\\&{\underline {\ \ 18\ \ }}\\&\ \ 15\end{aligned}}$

Nella lezione sulle quattro operazioni trovate il paragrafo dedicato alla spiegazione della [divisione con il resto]

Divisibilità

Un numero naturale n è divisibile per un altro numero naturale, m, se la divisione del primo, n il dividendo, per il secondo, m il divisore, da come resto 0. Usando la moltiplicazione il primo numero n risulta un multiplo del numero m. Ad esempio 72 è divisibile per 9 poiché

$72:9=8\ e\ resto\ r=0$

notiamo che come scritto sopra $72$ è un multiplo di $9$ infatti

$9\cdot 8=72$.

Divisori

Video per chi non ama leggere: Matteo Ruffoni, Divisori nei naturali(1), su YouTube, 28 gen 2019.

Criteri di divisibilità

In questo paragrafo vengono riportate in breve le regole utili a verificare la divisibilità tra i numeri. In genere ci si chiede se un numero, grande, scritto con più di tre cifre, è divisibile per un altro numero, piccolo, entro i primi 20 numeri della sequenza dei numeri naturali. Per comprendere il perché questi criteri funzionano è possibile approfondire lo studio alla pagina Criteri di divisibilità

Numeri divisibili per 2

Tutti i numeri pari sono divisibili per $2$. Il criterio afferma, ovviamente, che se un numero ha come ultima cifra $0$ oppure $2$ o $4$ o $6$ o $8$, essendo pari, allora è divisibile per 2.

Numeri divisibili per 3

Un numero è divibile per $3$ se la somma delle sue cifre è un numero a sua volta divisibile per $3$.
Ad esempio $7524$ è divisibile per $3$ infatti $7+5+2+4=18\rightarrow 1+8=9$ e $9$ è divisibile per $3$

Numeri divisibili per 4

$4$ è un divisore di un numero se le ultime due cifre del numero sono 00 oppure un multiplo di 4.

Multipli di $4$:

$M_{4}=\left\{04,08,12,16,20,24,28,32,36,40,44,48,52,56,60,64...\right\}$

Sono elencati solo alcuni dei multipli di $4$ con due cifre, compresi i primi due evidenziando lo $0$.

Numeri divisibili per 5

Tutti i multipli di $5$ devono obbligatoriamente avere l'ultima cifra uguale a $5$ o a $0$.
$M_{5}=\left\{5,10,15,20,25,30...\right\}$

Numeri divisibili per 6

Non è un criterio vero e proprio ma per essere un multiplo di $6$ un numero deve essere pari e divisibile per $3$, quindi il controllo si rivela piuttosto semplice.

Numeri divisibili per 7

Non esiste un criterio semplice per verificare se un numero è divisibile per 7: spesso il sistema più semplice è fare direttamente la divisione. Un metodo non eccessivamente complicato consiste nel partire dalla cifra più a sinistra, triplicarla, sommarla a quella successiva, e togliere eventuali multipli di 7. Continuando così fino all'ultima cifra, se il risultato finale è 0 (oppure 7) allora il numero è multiplo di 7, altrimenti no.

Prendiamo per esempio 31416. Al primo passo si calcola $3\cdot 3+1=10$, e togliendo i multipli di 7 rimane 3. Il secondo passo è $3\cdot 3+4=13$, e togliendo i multipli di 7 rimane 6. Il terzo passo è $6\cdot 3+1=19$, che togliendo 14 lascia 5. Infine $5\cdot 3+6=21$ che è un multiplo di 7; pertanto 31416 è multiplo di 7.

Numeri divisibili per 9

La divisibilità per $9$ si verifica in un modo simile a quella per $3$.
Se la somma delle cifre di un numero è divisibile per $9$ allora lo sarà anche il numero.
Ad esempio $7524$ è divisibile per $9$ infatti $7+5+2+4=18\rightarrow 1+8=9$ e $9$ è divisibile per $9$.

Numeri divisibili per $11$

Un numero è divisibile per $11$ se la differenza tra la somma delle sue cifre di posto dispari e la somma delle sue cifre di posto pari dà come risultato $0$, $11$ o un multiplo (anche intero) di $11$.
Ad esempio $2585$ poiché $\left(2+8\right)-\left(5+5\right)=10-10=0$ allora $2585$ è divisibile per $11$ infatti $2585:11=235$

Osservazioni sulla divisibilità

Divisibile per un multiplo allora...

Se un numero ha come divisore un multiplo di altri fattori allora è divisibile per ciascuno dei suoi sottomultipli. In altre parole se un numero è un divisore di un altro numero allora è divisore anche di ciascun multiplo del secondo.
ad esempio poichè $24$ è divisibile per $6$ e $6$ è a sua volta dvisibile sia per $3$ che per $2$ allora $24$ è divisibile anche per $3$ e per $2$

Non divisibile per un fattore allora...

Dalla prima osservazione si ricava di conseguenza che se un numero non è divisibile per una certo fattore allora non lo sarà nemmeno per i multipli del fattore. Ed in altre parole se un numero non è un divisroe di un certo altro numero allora non lo sono nemmeno i suoi multipli. I numeri che non sono divisibili per $3$ non lo sono nemmeno per $6$, per $9$, per $12$...

Divisibilità dei multipli

Se un numero ha un divisore allora anche tutti i suoi multipli lo avranno, ad esempio

$46=23\cdot 2\rightarrow 92=46\cdot 2$ quindi $92=23\cdot 4$

Divisibilità di numeri eprimibili come somma o differenza

Con un ragionamento simile a quello dei multipli si può osservare che un numero sarà divisibile per un certo divisore se lo si può ottenere sommando due multipli del divisore:

$1505$ è un multiplo di 7, scritto in simboli $1505\in M7$ 

poichè è

$1505=1470+35$ e i due addendi sono facilmente riconoscibili come multipli di $7$

infatti

$1470=1400+70=14\cdot 100+7\cdot 10=7\cdot 200+7\cdot 10=7\cdot 210$

e

$35=7\cdot 5$

quindi per la proprietà distributiva

$1505=7\cdot 215$

Questo ci permette di capire se numeri piuttosto grandi sono o meno divisibili per un dato divisore. Si cerca un numero vicino a quello da testare sicuramente divisibile per il divisore, si esprime il primo numero come somma o differenza e poi si controlla il secondo addendo, o nel caso della divisione il sottraendo. Se il secondo addendo, o il sottraendo, risulta a suo volta divisibile allora lo sarà anche il numero di partenza.

Esercizi per capire la divisibilità

1

12 è divisibile per

	2, 3, 4 e 6
	5 e 5 e 2
	2, 4 e 7

2

85 è divisibile per

	3
	5
	2

3

1416 è divisibile per

	3
	4
	5

4

319 è divisibile per

	7
	9
	11

5

84 è divisibile per

	6
	8
	9

6

84 è divisibile per

	16 poichè 80 lo è e 4 è sottomultiplo di 16
	8 poichè 84 = 8²
	7 poichè è 84 = 42 * 2

7

84 è divisibile per

	16 poichè 80 lo è e 4 è sottomultiplo di 16
	8 poichè 84 = 60 + 24 entrambi multipli di 8
	7 poichè è 84 = 70 + 14 entrambi multipli di 7

8

126 è divisibile per

	2 e 3 quindi anche per 5
	2 e 3 quindi anche per 6
	2 e 3 quindi anche per 23

9

147 è divisibile per

	7 infatti 140+7
	14 infatti 140= 14 * 10 e 7 fattore di 14
	è primo

10

96 è divisibile per

	solo per 2
	9 infatti è vicino a 99
	4 infatti 96 = 100 - 4 entrambi divisibili per 4

Esercizi per imparare la divisibilità

Questi esercizi vanno svolti su un quaderno e fatti correggere dall'insegnante o confrontati con i propri compagni.

Trovare i divisori

Mentre la ricerca dei multipli di un numero è semplice basta moltiplicare il numero per tutti gli altri. Ad esempio i multipli di $3$ sono:

$3\cdot 1=3$

$3\cdot 2=6$

$3\cdot 3=9$

...

$3\cdot 7=21$

...

E i multipli sono infiniti, mentre i divisori sono sicuramente limitati, il divisore più grande di un numero è il numero stesso, ad esempio il divisore più grande di $24$ è $24$, e il più piccolo è $1$.
Per trovare i divisori si deve applicare un metodo più complesso.

I divisori con il metodo Arcobaleno

Un metodo semplice per trovare i divisori di un numero $n$ è quello di provare le divisioni partendo da $1$ per arrivare fino al numero stesso $n$, in questo modo però i tentativi potrebbero rivelarsi tanti, forse troppi. Proviamo a creare un metdo che di permetta di ridurre il numero delle divisioni.

Per prima cosa si può osservare che i divisori di un numero si presentano sempre in coppia, infatti:

$24:4=6$ 

nell'esempio sono divisori di $24$ sia il divisore $4$ che il quoziente $6$.

Questa osservazione ci permette di ridurre in modo significativo i tentativi che dovremmo fare.

Video per chi non ama leggere: Maths how to, How to draw a factor rainbow to find the factors of 90., su YouTube, 28 lug 2022.

Per spiegare il metodo Arcobaleno usiamo un esempio e cerchiamo i divisori del numero $110$

L'idea è quella di testare i numeri in ordine crescente $(1,2,3...)$ tenendo conto delle osservazioni per evitare tentativi inutili.

Osserviamo che ogni numero è divisibile per $1$ e per se stesso.

$110:1=110$. La prima coppia è $(1,110)$.

Passiamo al $2$: È pari? Sì.

$110:2=55$. La seconda coppia è $(2,55)$.

Osserviamo che $55$ non è pari, dunque $110$ non è divisibile per $4$, poichè un numero divisibile per $4$ dovrebbe essere divisibile due volte per $2$, cioè dovrebbe essere possibile fare la metà della metà. Di conseguenza non sarà divisibile per tutti i multipli di $4$.
Testiamo il $3$? La somma delle cifre $(1+1+0=2)$ non rispetta il criterio di divisibilità per $3$, $110$ non è divisibile per $3$ nè er nessuno dei multipli di $3$.
Non proviamo per il $4$ per l'osservazione fatta prima.
Passiamo al $5$:

$110:5=22$. La terza coppia è $(5,22)$.

Non proviamo per il $6$ per l'osservazione fatta prima.
Proviamo il $7$, anche con la calcolatrice:

$110:7\approx 15,71...$. 

$110$ non è divisibile per $7$, cosa che si può dedurre anche dal fatto che $112=70+42$ è divisibile per $7$ e $112-110=2$ non è divisibile per $7$ e per le osservazioni fatte nei precedenti paragrafi.

$8$ e $9$ non li proviamo sono multipli di non divisori trovati prima.

Proviamo il $10$? Finisce per $0$ e dunque è divisibile.

$110:10=11$ Quindi sono divisori $(10,11)$.

Abbiamo finito? Il numero successivo sarebbe il $11$, ma lo abbiamo appena trovato nella divisione per $10$, quindi abbiamo finito poichè altri divisori altro non sarebbero che i quozienti delle divisioni precedenti.
Per darci una regola osserviamo che l'ultima divisione è quella nella quale il quoziente diventa più piccolo del divisore, da quella divisione in poi ulteriori divisori altro non sarebbero che i quozienti già trovati, nelle divisioni precedenti.

In conclusione i divisori di $110$ sono $\left\{1,\ 2,\ 5,\ 10,\ 11,\ 22,\ 55,\ 110\right\}$ e li abbiamo trovati svolgendo una decina di tentativi che sono molti di meno di 110.

Esercizi per imparare a trovare i divisori

• Scratch - Divisori game

Multipli, divisori e scomposizione in fattori

Tutti i numeri hanno multipli infiniti. Prendiamo ad esempio il 7 e vediamo che l'insieme dei multipli di 7 è

$M7=\left\{7,14,21,28,35,42....\right\}$

la sequenza continua all'infinito comprendendo tutti i multipli di 7.

Non è infinito invece l'insieme dei divisori di un numero, ad esempio 24

$D24=\left\{24,12,8,6,4,3,2,1\right\}$

Esistono numeri per i quali l'insieme dei divisori si riduce a due soli elementi, 1 e il numero stesso ad esempio 13

$D13=\left\{1,13\right\}$

per semplicità si dice che questi numeri non hanno divisori.

Numeri primi

I numeri primi sono che non hanno divisori, per essere maggiormente precisi, come abbiamo visto sopra, si possono dividere soltanto per 1 o per se stessi.

I primi numeri primi sono:

$2,3,5,7,11,13,17,19,23,...$

La sequenza è infinita, lo aveva dimostrato già Euclide.

Scomposizione in fattori primi

Se si esaminano tutti i numeri si scopre che o sono primi, oppure hanno divisori, e se hanno divisori si possono ottenere attraverso la moltiplicazione di alcuni dei loro divisori scelti tra numeri primi, anche se ripetuti. Questa moltiplicazione si chiama scomposizione in fattori primi, ed ha la particolarità di essere unica^VK. Ad esempio

$24=2\cdot 2\cdot 2\cdot 3=2^{3}\cdot 3$

Come si può trovare la scomposizione in fattori primi di un numero?

Partiamo dall'esempio qui sopra e scomponiamo 24 in una moltiplicazione di due fattori

$24=4\cdot 6$

a loro volta 4 e 6 possono essere scomposti

 $4=2\cdot 2=2^{2}$ e  $6=2\cdot 3$ 

$2$ e $3$ sono numeri primi che non possono essere scomposti in moltiplicazioni.
Quindi

$24=2^{2}\cdot 2\cdot 3=2^{3}\cdot 3$

Esercizi per capire la scomposizione in fattori primi

Qule è la corretta scomposizione in fattori primi di 12?

	$12=6\cdot 2$
	$12=2^{2}\cdot 3$
	$12=3\cdot 4$

Esercizi per imparare la scomposizione in fattori

• Fattorizzazione con Scratch
• Scomposizione ad albero

Massimo Comun Divisore

Il Massimo Comun Divisore è il divisore più grande tra i divisori comuni di due o più numeri, ed ovviamente i numeri di partenza risulteranno essere multipli del MCD. Ad esempio cerchiamo il MCD tra $12$ e $18$.

I divisori di $12$ sono : $D_{12}=\left\{1,2,3,4,6,12\right\}$; ed i divisori di $18$ sono : $D_{18}=\left\{1,2,3,6,9,18\right\}$.

Non è difficile individuare $6$ che è il divisore più grande presente in entrambi gli insiemi e concludere $\operatorname {MCD} (12,18)=6.$.

Usando una scrittura simbolica $\operatorname {MCD} (12,18)=max\left(D_{12}\cap D_{18}\right)=max\left\{1,2,3,6\right\}=6$

mcm e MCD

Incidentalmente osservando l'insieme intersezione dei divisori comuni di due numeri notiamo che non potrà mai essere vuoto. Il numero che comparirà sempre come elemento dell'intersezione degli insiemi dei divisori è il numero $1$
.

Quindi se anche due numeri non avessero nessun fattore diverso da $1$ in comune, avrebbero sempre come MCD il numero $1$.

Ad esempio :

$MCD(19,23)=1$

Ma come calcolare il MCD quando i numeri diventano più grandi?

Trovare MCD con la scomposizioni in fattori primi

Video per chi non ama leggere: Matteo Ruffoni, mcm e MCD scomposizione, su YouTube, 5feb 2020.

Ripetiamo, con scelta un po' noiosa, la ricerca del MCD tra $12$ e $18$ usando la scomposizione in fattori.

 $MCD(12,18)=?$

La scomposizione in fattori di $12$ è:

$12=2^{2}\cdot 3$,

e quella di $18$ è:

$18=2\cdot 3^{2}$.

Riscriviamo le scomposizioni senza usare le potenze mettendo in evidenza la presenza dei fattori comuni

$12=2\cdot \left(2\cdot 3\right)$ e  $18=\left(2\cdot 3\right)\cdot 3$.

Ed ecco evidente che la moltiplicazione

$2\cdot 3$ 

è presente in tutte e due le fattorizzazioni ed è la moltiplicazione più grande in comune, non ci sono altri fattori in comune che possono essere aggiunti.
Quindi:

  $MCD(12,18)=6$

Trovare MCD in casi particolarmente facili

Video per chi non ama leggere: Matteo Ruffoni, MCD a mente, su YouTube, 28 gen 2020.

Multipli

MCD 6 18

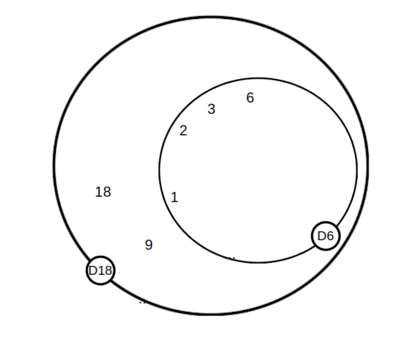
Se uno dei due numeri è multiplo dell'altro il MCD è ovviamente il numero più piccolo, il sottomultiplo, il divisore.

Ad esempio se cerco

$MCD(18,6)=?$

noto che tutti i divisori di $6$, esso compreso, sono divisori di $18$,

quindi il MCD è $6$.

$MCD(18,6)=6$

Multipli di un fattore comune evidente

Se cerco il MCD tra $2400$ e $1800$

è evidente che $100$ è un fattore comune tra i due numeri,

inoltre che

$MCD(18,24)=6$

posso facilmente concludere che

$MCD(1800,2400)=600$.

Trovare MCD con le divisioni successive

Video per chi non ama leggere: Matteo Ruffoni, MCD con divisioni successive, su YouTube, 31 gen 2020. Il metodo delle divisioni per trovare il MCD successive si basa sul fatto che dati due numeri, ad esempio $72$ e $30$, si può sempre fare la divisione, con il resto, del più grande per il più piccolo e quindi scrivere questa uguaglianza:

$72=30\cdot 2+12$,

infatti il $30$ ci sta $2$ volte nel $72$ e il resto è $12$.

Introducendo un po' di nomenclatura:

• $72$ è il dividendo
• $30$ è il divisore
• $2$ è il quoziente
• $12$ è il resto

quindi il dividendo è uguale al divisore moltiplicato il quoziente più il resto.

In una formula molto più generale dati $dividendo$ e $divisore$:

$dividendo=divisore\cdot quoziente+resto$.

Tornando all'esempio numerico

$72=30\cdot 2+12$,

notiamo che se un numero è sottomultiplo, divisore, di $72$ allora dovrà esserlo per forza anche del divisore $30$ e del resto $12$, cosa che abbiamo osservato nel paragrafo Divisibilità somma e differenza.

Prendiamo ad esempio $3$ dal fatto che

$72=3\cdot 24$ 

si deduce che

$72=3\cdot 24=30\cdot 2+12=3\cdot \left(10\cdot 2+4\right)$ 

cioè che se il dividendo ha un sottomultiplo, anche divisore e resto sono multipli dello stesso sottomultiplo.

Infatti:

• $72=3\cdot 24$
• $30=3\cdot 10$
• $12=3\cdot 4$

e questo vale anche per il MCD dei tre numeri, che nel nostro esempio è $6$, infatti:

• $72=6\cdot 12$
• $30=6\cdot 5$
• $12=6\cdot 2$

concludendo si può affermare che il MCD di $72$ e $30$ anche il MCD di $30$ e $12$

.

In termini più generali possiamo dire che per trovare il MCD di due numeri si può procedere alla divisione del più grande per il più piccolo e cercare poi il MCD tra il numero più piccolo e il resto della divisione appena effettuata.
Procedimento che si può ripetere fino a raggiungere la divisione che dà resto zero, in quel caso il MCD è il divisore di quest'ultima divisione.

Esempio numerico:

$MCD(1246,582)=?$

dalla divisione con resto

$1246:582=$

ottengo

$1246=582\cdot 2+82$

quindi

$MCD\left(1246,582\right)=MCD\left(582,82\right)$

$582=82\cdot 7+8$

e allora

$MCD\left(1246,582\right)=MCD\left(582,82\right)=MCD\left(82,8\right)$

$82=8\cdot 10+2$

e dunque

$MCD\left(1246,582\right)=MCD\left(582,82\right)=MCD\left(82,8\right)=MCD\left(8,2\right)$

e poiché

$8=2\cdot 4+0$

cioè è la divisione con resto zero,

posso concludere che

$MCD\left(1246,582\right)=MCD\left(582,82\right)=MCD\left(82,8\right)=MCD\left(8,2\right)=2$

$MCD\left(1246,582\right)=2$.

Esercizi per imparare il MCD

Video per chi non ama leggere: Matteo Ruffoni, MCD problema semplice, su YouTube, 28 gen 2020.

Minimo Comune Multiplo

Video per chi non ama leggere: Matteo Ruffoni, MCD e mcm, su YouTube, 15 feb 2019.

Il minimo comune multiplo è il multiplo più piccolo tra i multipli comuni di due o più numeri, ed ovviamente i numeri di partenza risulteranno essere divisori del mcm.

L'insieme dei multipli di un numero è un insieme infinito:

$M_{12}=\left\{12,24,36,48,60,72,...\right\}$

che ha come primo elemento il numero dato, ${12}$ nel nostro caso, e cresce poi con moltiplicazioni successive.

La ricerca del mcm comune multiplo di due numeri consiste nel trovare il più piccolo multiplo che compare in entrambi gli insiemi.

Ad esempio cerchiamo $\operatorname {mcm} (12;18)$

$M_{12}=\left\{12,24,36,48,60,72,...\right\}$

$M_{18}=\left\{18,36,54,72,...\right\}$

già dopo aver prodotto pochi multipli individuiamo il ${36}$, come mcm, quindi

$\operatorname {mcm} (12;18)=36$.

Mcm M12 M18

Trovare il $\operatorname {mcm}$ con la scomposizione in fattori

Per trovare il $\operatorname {mcm}$ di due numeri dobbiamo procedere con le scomposizioni in fattori e comporre poi la moltiplicazione con il minor numero di fattori che sia abbastanza grande per contenere le scomposizioni dei numeri iniziali.

$12=2^{2}\cdot 3$

$18=2\cdot 3^{2}$

quindi

$\operatorname {mcm} (12;18)=2^{2}\cdot 3^{2}=4\cdot 9=36$.

I fattori del $\operatorname {mcm}$ sono tutti quelli che compaiono nelle scomposizioni presi con l'esponente più grande.

Prendendo un altro esempio calcoliamo il

$\operatorname {mcm} (12;15)$

le scomposizione sono

$12=2^{2}\cdot 3$

$15=3\cdot 5$

quindi

$\operatorname {mcm} (12;15)=2^{2}\cdot 3\cdot 5=4\cdot 15=60$.
.

È questo secondo esempio conferma la regola generale.

Test riassuntivo su fattorizzazione, mcm e MCD

Punto aggiunto per ogni risposta corretta:
Punti sottratti per ogni risposta non corretta:
Ignora i coefficienti di domanda:

1

La scomposizione in fattori primi di $24$ è?

	$2^{2}\cdot 3$
	$2\cdot 3$
	$2^{3}\cdot 3$
	$6^{4}$

2

La scomposizione in fattori primi di $36$ è?

	$2^{2}\cdot 3^{2}$
	$4\cdot 9$
	$2^{3}\cdot 3$
	$6^{2}$

3

La scomposizione in fattori primi di $28$ è?

	$2\cdot 14$
	$2^{2}\cdot 7$
	$2^{3}\cdot 7$
	$14^{2}$

4

La scomposizione in fattori primi di $16$ è?

	$8^{2}$
	$2^{3}$
	$2^{4}$
	$10\cdot 6$

5

La scomposizione in fattori primi di $37$ è?

	$3^{3}$
	$3^{7}$
	$37$
	$2\cdot 3^{2}$

6

La scomposizione in fattori primi di $42$ è?

	$2^{2}\cdot 3$
	$2\cdot 3\cdot 7$
	$21\cdot 2$
	$7^{2}$

7

La scomposizione in fattori primi di $49$ è?

	$7^{2}$
	$4\cdot 9$
	$3^{3}$
	$7\cdot 2$

8

La scomposizione in fattori primi di $56$ è?

	$2^{2}\cdot 3\cdot 7$
	$5\cdot 6$
	$2^{3}\cdot 7$
	$5^{6}$

9

La scomposizione in fattori primi di $60$ è?

	$2^{2}\cdot 3\cdot 5$
	$6\cdot 10$
	$2^{3}\cdot 5$
	$6^{2}$

10

La scomposizione in fattori primi di $74$ è?

	$2^{2}\cdot 13$
	$2^{2}\cdot 19$
	$7\cdot 4$
	$7^{4}$

Bibliografia

• Contaci! - Clara Bertinetto, Arja Metiainen, Johannes Paasonen, Eija Voutilainen - Zanichelli - 2013- ISBN 978.88.08.06443.1

Collegamenti esterni

• w:Massimo comun divisore
• w:Criteri di divisibilità