Automi riconoscitori ed espressioni regolari

Lo scopo di questa lezione è presentare alcuni metodi per tradurre un'espressione regolare in un automa a stati finiti. Non esiste un metodo preciso e unico per effettuare questa operazione; i differenti algoritmi producono soluzioni diverse, alcuni deterministici altri no, altri con epsilon mosse altri no.

Introduciamo dapprima la classe dei linguaggi locali, che tornerà utile per alcuni algoritmi.

Linguaggi locali

Definiamo la classe dei linguaggi localmente testabili, chiamata anche semplicemente locale (LOC) come sottofamiglia (propria) dei linguaggi regolari $LOC\subset REG,\ LOC\not \equiv REG$. Per definirla facciamo uso delle seguenti "funzioni" di un linguaggio:

• insieme dei caratteri iniziali: $Ini(L)=\left\{\ a\in \Sigma \ |\ a\Sigma ^{*}\cap L\neq \varnothing \right\}$
• insieme dei caratteri finali: $Fin(L)=\left\{\ a\in \Sigma \ |\ \Sigma ^{*}a\cap L\neq \varnothing \right\}$
• insieme di digrammi: $Dig(L)=\left\{\ x\in \Sigma ^{2}\ |\ \Sigma ^{*}x\Sigma ^{*}\cap L\neq \varnothing \right\}$
• insieme complemento di digrammi: ${\overline {Dig}}(L)=\Sigma ^{2}\setminus Dig(L)$

Le operazioni sopra possono essere applicate con lo stesso effetto alla singola stringa anziché a un intero linguaggio.

Esempi

$L_{1}=(abcd)^{*}$

$Ini(L_{1})=\{a\}$

$Fin(L_{1})=\{d\}$

$Dig(L_{1})=\{ab,bc,cd,da\}$

$L_{2}=a^{*}b^{*}(cd)^{+}$

$Ini(L_{2})=\{a,b,c\}$

$Fin(L_{2})=\{d\}$

$Dig(L_{2})=\{aa,ab,ac,bb,bc,cd,dc\}$

$x=abc$

$Ini(x)=a$

$Fin(x)=c$

$Dig(x)={ab,bc}$

Definizione

Un linguaggio locale è un linguaggio che contiene tutte e solo le stringhe che possono essere generate a partire dai tre insiemi visti sopra:

$L\setminus \varepsilon =\{x\ |\ Ini(x)\in Ini(L)\land Dig(x)\subseteq Dig(L)\land Fin(x)\in Fin(L)\}$

Esempio1: $L_{1}=(abcd)^{*}$ è locale: tutte le stringhe ottenute da Ini, Fin e Dig sono contenute in $L_{1}$.

Esempio2: $L_{1}=(bb)^{*}c^{+}$ non è locale: la stringa bbbc non è contenuta in $L_{1}$ ma rispetta le condizioni sopra citate.

Per ogni $L$ regolare non locale, esiste un altro linguaggio $L_{LOC}$ regolare e locale che contiene tutte le stringhe ottenibili da $Ini(L),Fin(L),Dig(L)$.

Riconoscitore

Il riconoscitore dei linguaggi locali è molto semplice: devo verificare che il primo e ultimo carattere sia quelli cercati e che ogni coppia sia presente.

Vediamo come fare con un esempio, traduciamo il linguaggio locale: $L_{e}=(abc)^{+}$

$Ini(L_{e})=\{a\}$

$Fin(L_{e})=\{c\}$

$Dig(L_{e})=\{ab,bc,ca\}$

Metodi

Tra i molti metodi possibili, abbiamo:

• Metodo di Thompson o strutturale: l'automa generato è in generale non deterministico e con $\varepsilon$-mosse.
• Metodo GMY (Glushhkov, Mc Naugthon and Yamada): l'automa generato è in generale non deterministico ma senza $\varepsilon$-mosse.
• Metodo BS (Berry and Sethi): automa deterministico

Metodo di Thompson

L'idea del metodo Thompson è elaborare le varie componenti dell'automa partendo dalla regex ed analizzandola parte per parte. Successivamente le componenti verranno interconnesse in modo da ottenere un riconoscitore completo.

N.B. il metodo di Thompson funziona solo se assumiamo un solo stato iniziale e un solo stato finale senza, rispettivamente, archi entranti o uscenti. Nel caso in cui questo non fosse vero, è necessario sostituire con (ovvero aggiungere) un nuovo stato iniziale e/o finale per riportarci alla situazione desiderata.

L'algoritmo consiste nel prendere ogni singolo elemento della regex ed applicarne le regole seguenti per generare un piccolo automa che verrà poi assemblato:

L'espressione $e=\varepsilon$ è rappresentata dall'automa

Un simbolo $e=a$ è convertito nell'automa:

L'espressione ottenuta dall'unione di due sottoespressioni $e=s|t$ è convertita in

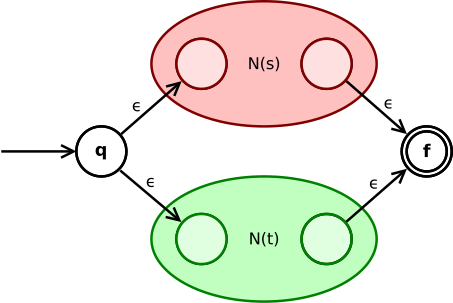
Lo stato $q$ va tramite un' $\varepsilon$-transazione in uno stato iniziale di $N(s)$ o $N(t)$. I loro stati finali divengono intermedi e si uniscono per mezzo di $\varepsilon$-transazioni nello stato finale di N(e) chiamato $f$.

L'espressione formata dalla concatenazione di due sottoespressioni $e=st$ si converte in

Lo stato iniziale di $N(s)$ è lo stato iniziale di N(e). Lo stato finale di $N(s)$ diventa lo stato iniziale di $N(t)$. lo stato finale di $N(t)$ è anche lo stato finale di $N(e)$.

La Kleene star di un'espressione $e=s^{*}$ è convertita in

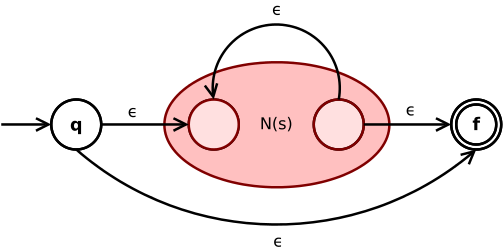
Un' $\varepsilon$-transizione connette lo stato iniziale e finale dell' NFA $N(e)$. Un'altra $\varepsilon$-transizione che va dallo stato finale a quello iniziale di $N(s)$ consente la ripetizione dell'espressione $s$ come da definizione dell'operatore Kleene star.

Metodo BS

Per il metodo BS sfrutteremo i linguaggi locali definiti nella prima sezione. Ricordiamo che il grande vantaggio di questo metodo è che l'automa generato è deterministico. Introduciamo questo algoritmo tramite un esempio.

Si prenda la seguente regex:

$e=(x|yy)^{*}(xz)^{+}$

e la sua versione numerata terminata (ovvero con un carattere alla fine chiamato terminatore $\dashv$):

$e'=(x_{1}|y_{2}y_{3})^{*}(x_{4}z_{5})^{+}\dashv$

Definiamo insieme dei successori di un carattere come segue:

$Fol(a_{i})\ :=\ \{\ b_{j}\ |\ a_{i}b_{j}\in Dig(e')\ \}$

Risulterà quindi che il terminatore è il carattere che segue tutti i caratteri finali

$\dashv \in Fol(a_{i}),\ \ \forall a_{i}\in Fin(e')$

$Fol(\dashv )=\varnothing$

(abbiamo usato un abuso di notazione, il carattere terminatore non è propriamente parte della regex, altrimenti sarebbe da considerare il finale)

Nel precedente esempio risulterà: $Fol(x_{1})=\{x_{1},y_{2},x_{4}\}$, $Fol(y_{2})=\{y_{3}\}$, $Fol(z_{5})=\{x_{4},\dashv \}$, ...

Ogni insieme $Fol()$ corrisponde all'insieme dei simboli che si aspettano come prossimo input e il terminatore rappresenta lo stato finale. Di conseguenza lo stato iniziale risulta: $Ini(e'\dashv )$.

Si applica in seguente algoritmo:

$Q=Ini(e'\dashv )$

$\delta =\varnothing$

${\textbf {WHILE}}{\text{ esiste uno stato }}q\in Q{\text{ non visitato }}{\textbf {DO}}$

${\text{setta }}q{\text{ visitato }}$

${\textbf {FOREACH}}{\text{ simbolo }}b\in \Sigma {\text{ terminale }}{\textbf {DO}}$

$q'=\bigcup _{\forall b_{i}\in q}Fol(b_{i})$

${\textbf {IF}}\ q'\neq \varnothing \ {\textbf {THEN}}$

${\textbf {IF}}\ q'\notin Q\ {\textbf {THEN}}$

${\text{setta }}q'{\text{ NON visitato }}$

$Q=Q\cup q'$

${\textbf {ENDIF}}$

$\delta =\delta \cup {q{\overset {b}{\to }}q'}$

${\textbf {ENDIF}}$

${\textbf {DONE}}$

${\textbf {DONE}}$

L'algoritmo BS può anche essere usato per rendere un automa deterministico, anche se l'automa non deterministico di partenza possiede $\varepsilon$-mosse. L'idea è la seguente:

1. si ottiene una versione numerata dell'automa, aggiungendo anche un numero ad ogni $\varepsilon$-mossa;
2. si calcolino similmente alle regex gli insieme Ini e Fol;
3. utilizzando BS si ottenga il nuovo automa deterministico.