Per risolvere i triangoli qualsiasi, tramite l’altezza, bisogna ricercare all’interno della figura considerata dei triangoli rettangoli. Nel seguito saranno indicati altri teoremi che permettono di risolvere tutti i tipi di triangoli.
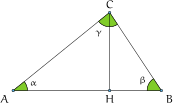
ESERCIZIO 1. Risolvi il triangolo acutangolo della figura con
α
=
39
°
{\displaystyle \alpha =39{\text{°}}}
β
=
57
°
{\displaystyle \beta =57{\text{°}}}
C
H
¯
=
11
m
{\displaystyle {\overline {CH}}=11{\text{m}}}
Risoluzione di un traingolo qualunque Ricordando che la somma degli angoli di un triangolo è
180
°
{\displaystyle 180{\text{°}}}
γ
{\displaystyle \gamma }
γ
=
180
°
−
α
−
β
=
180
°
−
39
°
−
57
°
=
84
°
.
{\displaystyle \gamma =180{\text{°}}-\alpha -\beta =180{\text{°}}-39{\text{°}}-57{\text{°}}=84{\text{°}}.}
Individuiamo ora i triangoli rettangoli nella figura in modo da poter applicare le formule.
Con il triangolo rettangolo
C
H
B
{\displaystyle CHB}
sin
(
β
)
=
C
H
¯
C
B
¯
⇒
C
B
¯
=
C
H
¯
sin
(
β
)
=
11
sin
(
57
°
)
≃
[
m
]
13
,
2
;
tan
(
β
)
=
C
H
¯
B
H
¯
⇒
B
H
¯
=
C
H
¯
tan
(
β
)
=
11
tan
(
57
°
)
≃
[
m
]
7
,
15
.
{\displaystyle {\begin{aligned}&\sin(\beta )={\tfrac {\overline {CH}}{\overline {CB}}}\quad \Rightarrow \quad {\overline {CB}}={\tfrac {\overline {CH}}{\sin(\beta )}}={\tfrac {11}{\sin(57{\text{°}})}}\simeq [m]{13,2};\\&\tan(\beta )={\tfrac {\overline {CH}}{\overline {BH}}}\quad \Rightarrow \quad {\overline {BH}}={\tfrac {\overline {CH}}{\tan(\beta )}}={\tfrac {11}{\tan(57{\text{°}})}}\simeq [m]{7,15}.\end{aligned}}}
Con il triangolo rettangolo
A
H
C
{\displaystyle AHC}
sin
(
α
)
=
C
H
¯
A
C
¯
⇒
A
C
¯
=
C
H
¯
sin
(
α
)
=
11
sin
(
39
°
)
≃
[
m
]
17
,
46
;
tan
(
α
)
=
C
H
¯
A
H
¯
⇒
A
H
¯
=
C
H
¯
tan
(
β
)
=
11
tan
(
39
°
)
≃
[
m
]
13
,
75
.
{\displaystyle {\begin{aligned}&\sin(\alpha )={\tfrac {\overline {CH}}{\overline {AC}}}\quad \Rightarrow \quad {\overline {AC}}={\tfrac {\overline {CH}}{\sin(\alpha )}}={\tfrac {11}{\sin(39{\text{°}})}}\simeq [m]{17,46};\\&\tan(\alpha )={\tfrac {\overline {CH}}{\overline {AH}}}\quad \Rightarrow \quad {\overline {AH}}={\tfrac {\overline {CH}}{\tan(\beta )}}={\tfrac {11}{\tan(39{\text{°}})}}\simeq [m]{13,75}.\end{aligned}}}
Infine calcoliamo
A
B
¯
=
A
H
¯
+
B
H
¯
≃
7
,
15
+
13
,
75
=
20
,
9
m
{\displaystyle {\overline {AB}}={\overline {AH}}+{\overline {BH}}\simeq {7,15}+{13,75}={20,9}{\text{m}}}
ESEMPIO 2. Nel trapezio rettangolo
A
B
C
D
{\displaystyle ABCD}
B
C
{\displaystyle BC}
35
°
{\displaystyle 35{\text{°}}}
A
B
{\displaystyle AB}
A
C
{\displaystyle AC}
B
C
{\displaystyle BC}
10
cm
{\displaystyle 10{\text{cm}}}
Risoluzione di un trapezio rettangolo Ricordando che la somma degli angoli di un triangolo è
180
°
{\displaystyle 180{\text{°}}}
C
A
B
^
=
55
°
{\displaystyle {\widehat {CAB}}=55{\text{°}}}
D
A
C
^
=
D
A
B
^
−
C
A
B
^
=
90
°
−
55
°
{\displaystyle {\widehat {DAC}}={\widehat {DAB}}-{\widehat {CAB}}=90{\text{°}}-55{\text{°}}}
C
B
{\displaystyle CB}
A
B
{\displaystyle AB}
D
C
{\displaystyle DC}
sin
(
A
B
C
^
)
=
A
D
¯
C
B
¯
⇒
C
B
¯
=
A
D
¯
sin
(
A
B
C
^
)
=
10
sin
(
35
°
)
≃
[
c
m
]
17
,
43
;
A
B
¯
=
C
B
¯
cos
(
A
B
C
^
)
≃
17
,
43
cos
(
55
°
)
≃
[
c
m
]
21
,
28
;
D
C
¯
A
D
¯
=
tan
(
D
A
C
^
)
⇒
D
C
¯
=
A
D
¯
⋅
tan
(
D
A
C
^
)
=
10
tan
(
35
°
)
≃
7
,
00
.
{\displaystyle {\begin{aligned}&\sin({\widehat {ABC}})={\tfrac {\overline {AD}}{\overline {CB}}}\quad \Rightarrow \quad {\overline {CB}}={\tfrac {\overline {AD}}{\sin({\widehat {ABC}})}}={\tfrac {10}{\sin(35{\text{°}})}}\simeq [cm]{17,43};\\&{\overline {AB}}={\tfrac {\overline {CB}}{\cos({\widehat {ABC}})}}\simeq {\tfrac {17,43}{\cos(55{\text{°}})}}\simeq [cm]{21,28};\\&{\tfrac {\overline {DC}}{\overline {AD}}}=\tan({\widehat {DAC}})\quad \Rightarrow \quad {\overline {DC}}={\overline {AD}}\cdot \tan({\widehat {DAC}})=10\tan(35{\text{°}})\simeq {7,00}.\end{aligned}}}
Da cui:
2
p
=
A
B
¯
+
B
C
¯
+
D
C
¯
+
D
A
¯
≃
21
,
28
+
17
,
43
+
7
,
00
+
10
=
[
c
m
]
55
,
71
;
Area
=
(
A
B
¯
+
D
C
¯
)
⋅
A
D
¯
2
≃
(
21
,
28
+
7
,
00
)
⋅
10
2
≃
[
c
m
2
]
141
,
40
.
{\displaystyle {\begin{aligned}&2p={\overline {AB}}+{\overline {BC}}+{\overline {DC}}+{\overline {DA}}\simeq {21,28}+{17,43}+{7,00}+10=[cm]{55,71};\\&{\text{Area}}\;={\tfrac {({\overline {AB}}+{\overline {DC}})\cdot {\overline {AD}}}{2}}\simeq {\tfrac {({21,28}+{7,00})\cdot 10}{2}}\simeq [cm^{2}]{141,40}.\end{aligned}}}
La topografia è una disciplina che studia gli strumenti ed i metodi operativi, sia di calcolo che di disegno, necessari per ottenere una rappresentazione grafica di una parte della superficie terrestre. La topografia ha carattere applicativo e trae la sua base teorica dalla matematica, dalla geometria e dalla trigonometria.
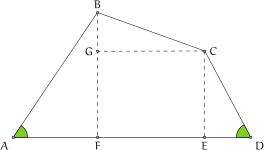
ESEMPIO 3. Risolvere il quadrilatero della figura [fig:C.7] sapendo che
A
B
=
42
,
5
m
{\displaystyle AB={42,5}{\text{m}}}
B
C
=
32
,
18
m
{\displaystyle BC={32,18}{\text{m}}}
C
D
=
27
,
6
m
{\displaystyle CD={27,6}{\text{m}}}
B
A
D
^
=
56
°
{\displaystyle {\widehat {BAD}}=56{\text{°}}}
A
D
C
^
=
62
°
{\displaystyle {\widehat {ADC}}=62{\text{°}}}
Risoluzione di un quadrilatero Dati :
A
B
¯
=
42
,
5
m
{\displaystyle {\overline {AB}}={42,5}{\text{m}}}
B
C
¯
=
32
,
18
m
{\displaystyle \quad {\overline {BC}}={32,18}{\text{m}}}
C
D
¯
=
27
,
6
m
{\displaystyle \quad {\overline {CD}}={27,6}{\text{m}}}
B
A
D
^
=
56
°
{\displaystyle \quad {\widehat {BAD}}=56{\text{°}}}
A
D
C
^
=
62
°
{\displaystyle \quad {\widehat {ADC}}=62{\text{°}}}
Obiettivo :
A
D
¯
{\displaystyle {\overline {AD}}}
A
B
C
^
{\displaystyle \quad {\widehat {ABC}}}
C
D
A
^
{\displaystyle \quad {\widehat {CDA}}}
Procedura risolutiva : Suddividiamo il quadrilatero in tre triangoli rettangoli e in un rettangolo, come nella figura, e risolviamo i triangoli.
Triangolo
F
B
A
{\displaystyle FBA}
F
{\displaystyle F}
F
B
A
^
=
90
°
−
B
A
D
^
=
90
°
−
56
°
=
34
°
;
A
F
¯
=
A
B
¯
cos
(
B
A
D
^
)
=
42
,
5
cos
(
56
°
)
≃
23
,
77
m
;
B
F
¯
=
A
B
¯
sin
(
B
A
D
^
)
=
42
,
5
sin
(
56
°
)
≃
35
,
23
m
.
{\displaystyle {\begin{aligned}&{\widehat {FBA}}=90{\text{°}}-{\widehat {BAD}}=90{\text{°}}-56{\text{°}}=34{\text{°}};\\&{\overline {AF}}={\overline {AB}}\cos({\widehat {BAD}})={42,5}\cos(56{\text{°}})\simeq {23,77}{\text{m}};\\&{\overline {BF}}={\overline {AB}}\sin({\widehat {BAD}})={42,5}\sin(56{\text{°}})\simeq {35,23}{\text{m}}.\end{aligned}}}
Triangolo
D
C
E
{\displaystyle DCE}
E
{\displaystyle E}
D
C
E
^
=
90
°
−
A
D
C
^
=
90
°
−
62
°
=
28
°
;
D
E
¯
=
C
D
¯
cos
(
F
B
A
^
)
=
27
,
6
cos
(
62
°
)
≃
12
,
96
m
;
C
E
¯
=
C
D
¯
sin
(
A
D
C
^
)
=
27
,
6
sin
(
62
°
)
≃
24
,
37
m
.
{\displaystyle {\begin{aligned}&{\widehat {DCE}}=90{\text{°}}-{\widehat {ADC}}=90{\text{°}}-62{\text{°}}=28{\text{°}};\\&{\overline {DE}}={\overline {CD}}\cos({\widehat {FBA}})={27,6}\cos(62{\text{°}})\simeq {12,96}{\text{m}};\\&{\overline {CE}}={\overline {CD}}\sin({\widehat {ADC}})={27,6}\sin(62{\text{°}})\simeq {24,37}{\text{m}}.\end{aligned}}}
Triangolo
G
B
C
{\displaystyle GBC}
G
{\displaystyle G}
B
G
¯
=
B
F
¯
−
G
F
¯
=
B
F
¯
−
C
E
¯
≃
35
,
23
−
24
,
37
≃
10
,
86
m
;
cos
(
C
B
G
^
)
=
B
G
¯
B
C
¯
≃
10
,
86
32
,
18
≃
0
,
34
⇒
C
B
G
^
=
cos
−
1
(
0
,
34
)
≃
70
°
16
′
36
″
;
B
C
G
^
=
90
°
−
C
B
G
^
≃
90
°
−
70
°
16
′
36
″
≃
19
°
43
′
24
″
;
G
C
¯
=
B
C
¯
sin
(
C
B
G
^
)
≃
B
C
¯
sin
(
70
°
16
′
36
″
)
≃
30
,
29
m
.
{\displaystyle {\begin{aligned}&{\overline {BG}}={\overline {BF}}-{\overline {GF}}={\overline {BF}}-{\overline {CE}}\simeq {35,23}-{24,37}\simeq {10,86}{\text{m}};\\&\cos({\widehat {CBG}})={\tfrac {\overline {BG}}{\overline {BC}}}\simeq {\tfrac {10,86}{32,18}}\simeq {0,34}\Rightarrow {\widehat {CBG}}=\cos ^{-}1({0,34})\simeq 70{\text{°}}16'36'';\\&{\widehat {BCG}}=90{\text{°}}-{\widehat {CBG}}\simeq 90{\text{°}}-70{\text{°}}16'36''\simeq 19{\text{°}}43'24'';\\&{\overline {GC}}={\overline {BC}}\sin({\widehat {CBG}})\simeq {\overline {BC}}\sin(70{\text{°}}16'36'')\simeq {30,29}{\text{m}}.\end{aligned}}}
Calcoliamo ora gli elementi incogniti del quadrilatero:
D
A
¯
=
A
F
¯
+
F
E
¯
+
E
D
¯
≃
23
,
77
+
30
,
29
+
12
,
96
=
67
,
02
m
;
A
B
C
^
=
A
B
F
^
+
F
B
C
^
≃
34
°
+
70
°
16
′
36
″
=
104
°
16
′
36
″
;
B
C
D
^
=
B
C
G
^
+
G
C
E
^
+
E
C
D
^
≃
19
°
43
′
24
″
+
90
°
+
34
°
=
143
°
43
′
24
″
.
{\displaystyle {\begin{aligned}&{\overline {DA}}={\overline {AF}}+{\overline {FE}}+{\overline {ED}}\simeq {23,77}+{30,29}+{12,96}={67,02}{\text{m}};\\&{\widehat {ABC}}={\widehat {ABF}}+{\widehat {FBC}}\simeq 34{\text{°}}+70{\text{°}}16'36''=104{\text{°}}16'36'';\\&{\widehat {BCD}}={\widehat {BCG}}+{\widehat {GCE}}+{\widehat {ECD}}\simeq 19{\text{°}}43'24''+90{\text{°}}+34{\text{°}}=143{\text{°}}43'24''.\end{aligned}}}










![{\displaystyle {\begin{aligned}&\sin(\beta )={\tfrac {\overline {CH}}{\overline {CB}}}\quad \Rightarrow \quad {\overline {CB}}={\tfrac {\overline {CH}}{\sin(\beta )}}={\tfrac {11}{\sin(57{\text{°}})}}\simeq [m]{13,2};\\&\tan(\beta )={\tfrac {\overline {CH}}{\overline {BH}}}\quad \Rightarrow \quad {\overline {BH}}={\tfrac {\overline {CH}}{\tan(\beta )}}={\tfrac {11}{\tan(57{\text{°}})}}\simeq [m]{7,15}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08ed5531959a86d82519cb76206f2e1c59794546)

![{\displaystyle {\begin{aligned}&\sin(\alpha )={\tfrac {\overline {CH}}{\overline {AC}}}\quad \Rightarrow \quad {\overline {AC}}={\tfrac {\overline {CH}}{\sin(\alpha )}}={\tfrac {11}{\sin(39{\text{°}})}}\simeq [m]{17,46};\\&\tan(\alpha )={\tfrac {\overline {CH}}{\overline {AH}}}\quad \Rightarrow \quad {\overline {AH}}={\tfrac {\overline {CH}}{\tan(\beta )}}={\tfrac {11}{\tan(39{\text{°}})}}\simeq [m]{13,75}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65f8b02285d0897d10ab351970640e050f6fdf84)











![{\displaystyle {\begin{aligned}&\sin({\widehat {ABC}})={\tfrac {\overline {AD}}{\overline {CB}}}\quad \Rightarrow \quad {\overline {CB}}={\tfrac {\overline {AD}}{\sin({\widehat {ABC}})}}={\tfrac {10}{\sin(35{\text{°}})}}\simeq [cm]{17,43};\\&{\overline {AB}}={\tfrac {\overline {CB}}{\cos({\widehat {ABC}})}}\simeq {\tfrac {17,43}{\cos(55{\text{°}})}}\simeq [cm]{21,28};\\&{\tfrac {\overline {DC}}{\overline {AD}}}=\tan({\widehat {DAC}})\quad \Rightarrow \quad {\overline {DC}}={\overline {AD}}\cdot \tan({\widehat {DAC}})=10\tan(35{\text{°}})\simeq {7,00}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/552b770208fe31eee281ca6d010fd58f5163b182)
![{\displaystyle {\begin{aligned}&2p={\overline {AB}}+{\overline {BC}}+{\overline {DC}}+{\overline {DA}}\simeq {21,28}+{17,43}+{7,00}+10=[cm]{55,71};\\&{\text{Area}}\;={\tfrac {({\overline {AB}}+{\overline {DC}})\cdot {\overline {AD}}}{2}}\simeq {\tfrac {({21,28}+{7,00})\cdot 10}{2}}\simeq [cm^{2}]{141,40}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccca50a62950ba77f7befba2e52da2b7a3b272d8)






















