Gli Angoli Particolari (superiori)

Possiamo ricavare per via geometrica il valore esatto delle funzioni trigonometriche di angoli particolari.

Angoli di 45°

Triangolo rettangolo isoscele

Il triangolo rettangolo isoscele ha gli angoli acuti di $45{\text{°}}$ ed è la metà di un quadrato di lato $l$. Sappiamo che $d={\sqrt {l^{2}+l^{2}}}={\sqrt {2l^{2}}}={\sqrt {2}}l$; poiché il calcolo delle funzioni trigonometriche per un angolo non dipende dal particolare triangolo usato, possiamo concludere per le definizioni date: $\sin(45{\text{°}})={\tfrac {l}{{\sqrt {2}}l}}={\tfrac {1}{\sqrt {2}}}={\tfrac {\sqrt {2}}{2}}$ e anche $\cos(45{\text{°}})={\tfrac {\sqrt {2}}{2}}$ e per la definizione di tangente dell’angolo $\tan(45{\text{°}})=1$.

Angoli di 30° e 60°

Triangolo rettangolo con angoli di 30 e 60 gradi

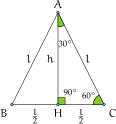
Il triangolo rettangolo con un angolo di $30{\text{°}}$ ha l’altro angolo acuto di $60{\text{°}}$ pertanto possiamo trattare insieme la ricerca delle funzioni trigonometriche di tali angoli.

Il triangolo rettangolo in questione è la metà di un triangolo equilatero di lato $l$ e altezza $h$; poiché ${\overline {HC}}$ è metà del lato possiamo subito dire che $\cos(60{\text{°}})={\tfrac {\overline {HC}}{l}}={\tfrac {l/2}{l}}={\tfrac {1}{2}}$. Per le definizioni date si ha $\sin(60{\text{°}})={\tfrac {\overline {AH}}{l}}$. Applicando il teorema di Pitagora si ottiene

${\overline {AH}}={\sqrt {l^{2}-\left({\tfrac {l}{2}}\right)^{2}}}={\sqrt {l^{2}-{\tfrac {l^{2}}{4}}}}={\sqrt {\tfrac {3}{4}}}l={\tfrac {\sqrt {3}}{\sqrt {4}}}l={\tfrac {\sqrt {3}}{2}}l\quad \Rightarrow \quad \sin(60{\text{°}})={\tfrac {\sqrt {3}}{2}}.$

Infine $\tan(60{\text{°}})={\tfrac {\sin(60{\text{°}})}{\cos(60{\text{°}})}}={\sqrt {3}}$.

Ricordando che per angoli complementari è $\sin(x)=\cos(90{\text{°}}-x)$ e $\cos(x)=\sin(90{\text{°}}-x)$ ed essendo $30{\text{°}}=90{\text{°}}-60{\text{°}}$ possiamo scrivere:

$\sin(30{\text{°}})=\cos(60{\text{°}})={\tfrac {1}{2}};\qquad \cos(30{\text{°}})=\sin(60{\text{°}})={\tfrac {\sqrt {3}}{2}}$

e infine

$\tan(30{\text{°}})={\cfrac {\tfrac {1}{2}}{\tfrac {\sqrt {3}}{2}}}={\tfrac {1}{\sqrt {3}}}={\tfrac {\sqrt {3}}{3}}.$

Angoli di 0° e 90°

Triangolo rettangolo

Ovviamente non esiste un triangolo con un angolo di $0{\text{°}}$: si tratta di un triangolo che degenera in un segmento. Possiamo pensare ad un triangolo rettangolo come nella figura, avente $a=1$ e immaginare di muovere il vertice $C$ in modo da rimpicciolire sempre più l’angolo $\beta$; quando $\beta$ diventa $0{\text{°}}$ il segmento $b$ si riduce ad un punto e si ha $b=0$ e quindi $sin(0{\text{°}})=0$, l’ipotenusa $a$ coincide con il cateto $c$ quindi $\cos(0{\text{°}})=1$ e infine $\tan(0{\text{°}})=0$.

Allo stesso modo, se deformiamo il triangolo fino ad avere l’angolo $\gamma$ di $0{\text{°}}$, quindi $\beta$ di $90{\text{°}}$, otteniamo che $\sin(90{\text{°}})=1$ e $\cos(90{\text{°}})=0$; applicando la formula della tangente si avrà una frazione con denominatore nullo e quindi diremo che $\tan(90{\text{°}})$ non è definita.

Possiamo riassumere i valori trovati per questi angoli particolari in una tabella:

${\begin{array}{cccc}{\text{angolo}}\,x&\sin(x)&\cos(x)&\tan(x)\\0{\text{°}}&0&1&0\\[2pt]30{\text{°}}&{\tfrac {1}{2}}&{\tfrac {\sqrt {3}}{2}}&{\tfrac {\sqrt {3}}{3}}\\[8pt]45{\text{°}}&{\tfrac {\sqrt {2}}{2}}&{\tfrac {\sqrt {2}}{2}}&1\\[8pt]60{\text{°}}&{\tfrac {\sqrt {3}}{2}}&{\tfrac {1}{2}}&{\sqrt {3}}\\[7pt]90{\text{°}}&1&0&{\text{non definita}}\\\end{array}}$

Come possiamo ottenere i valori delle funzioni trigonometriche per angoli diversi da quelli sopra considerati?