Esercitazione n°2: azioni esterne
Le azioni esterne (chiamate anche carichi) agenti sulle costruzioni possono essere suddivise in due grandi categorie:
- azioni esterne concentrate
- azioni esterne distribuite
A seconda dell'appartenenza delle azioni alla prima o alla seconda famiglia abbiamo diversi comportamenti interni della struttura (si veda la lezione relativa alle azioni interne).
Carichi concentrati
[modifica]I carichi concentrati, chiamati anche carichi puntiformi, sono quei carichi agenti su una porzione ridotta di elemento strutturale (nei nostri casi il solido trave). Essi possono essere sostanzialmente di due tipi:
- forze concentrate
- momenti concentrati
Forze concentrate
[modifica]Sono quelle forze, rappresentate con dei vettori, agenti in un punto preciso della struttura. Un esempio per comprendere quando si ha a che fare con un carico concentrato è rappresentato in figura: sulla trave orizzontale (rappresentata in giallo) grava il pilastro (le cui dimensioni si suppongono molto minori rispetto alla lunghezza della trave) rappresentato in rosso.

I carichi agenti sul pilastro (supponiamo valgano 500kN) si scaricano sulla trave in un punto ben preciso (il punto d'appoggio del pilastro rosso) interessandone quindi una porzione molto limitata. Se andiamo adesso a rappresentare la trave ed i pilastri tramite le sole linee d'asse sul piano bidimensionale otteniamo un disegno come quello rappresentato qui sotto:
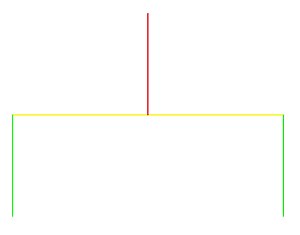
Se adesso volessimo andare a schematizzare il pilastro rosso otterremmo la situazione rappresentata qui sotto, dove il carico è stato sostituito con una forza di valore 500kN agente nella mezzeria (così viene chiamato in ingegneria il punto di mezzo della trave gialla).

Possiamo quindi notare come il carico del pilastro sia per la trave un carico concentrato.
Momenti concentrati
[modifica]I momenti concentrati sono indicati con una freccia ricurva in modo del tutto analogo alla reazione vincolare M.
Carichi distribuiti
[modifica]Osserviamo ora la situazione rappresentata in figura, nella quale il pilastro dell'esempio precedente è sostituito con un muro di trasversali non più trascurabili.

In tal caso, il carico di 500kN visto nel caso precedente non può più essere visto come una forza concentrata agente in mezzeria, in quanto l'area sulla quale questa forza agisce non è più trascurabile.

Al contrario, indicata con l la lunghezza del muro (e facendo l'ipotesi di lavorare in due dimensioni!) possiamo dire che ogni unità di lunghezza di trave risente di un carico pari al rapporto tra il carico complessivo P e l'area (o nel nostro caso, la lunghezza) del tratto di trave sul quale questo carico agisce.
La nuova grandezza q sarà quindi dimensionalmente uguale ad una forza divisa per una lunghezza (o per un'area), quindi avrà come unità di misura oppure .
Nel caso più generale possiamo avere una situazione come quella rappresentata in figura, dove l'andamento del carico distribuito in funzione dell'ascissa x può essere agevolmente espresso attraverso una funzione .

Se vogliamo andare a calcolare il valore complessivo del carico P dobbiamo calcolare il vettore risultante di questa distribuzione di forze; dovremo quindi risolvere l'integrale
Rimane ora il problema di dove posizionare il vettore risultante. Si tratta di una composizione di forze equiverse (sono tutti vettori che hanno lo stesso verso) e quindi il vettore risultante starà all'interno del segmento di lunghezza l sul quale agisce il carico, ed in particolare passerà per il baricentro della figura piana individuata dall'andamento della funzione (la parte di piano che, nelle figure relative ai carichi distribuiti, erano interessate dalle frecce). Ne consegue un ulteriore difficoltà relativa al calcolo del baricentro di una figura complessa come quella rappresentata nella figura sopra.
Se però andiamo a considerare il fatto che, in ingegneria, difficilmente avremo situazioni limite come quella appena presa in esame ci rendiamo conto che il calcolo del punto di applicazione del vettore risultante di un carico distribuito non presenta particolari difficoltà di calcolo. Le situazioni tipiche che si presenteranno durante tutto il corso sono rappresentate in figura:

Nel primo caso, chiamato carico rettangolare il modulo del vettore risultante è uguale a ed il vettore è applicato a metà del segmento di carico, ovvero di l. Nel secondo caso invece il valore del carico complessivo sarà applicato ad un terzo del segmento di carico partendo dal punto di massimo (punto nel quale è posizionato il baricentro del triangolo rettangolo).









