Esercitazione: le caratteristiche della sollecitazione

Esercizio 1

Si determinino le caratteristiche della sollecitazione della struttura illustrata in figura:

Siano:

$F\;=\;5KN$

$l\;=\;2m$

$\alpha \;=\;53^{\circ }$

Analisi cinematica

Nota:
Inserire analisi cinematica

Determinazione delle reazioni vincolari

Per determinare le reazioni vincolari sia interne che esterne agenti sulla struttura si sostituiscono i vincoli con le rispettive reazioni ipotizzando in maniera del tutto arbitraria dei segni alle reazioni stesse. Per facilitare i calcoli, inoltre, si sostituisce la forza esterna agente con le sue due componenti orizzontale e verticale, le quali avranno intensità:

$F_{H}=F\cos \alpha =3KN$
$F_{V}=F\sin \alpha =4KN$

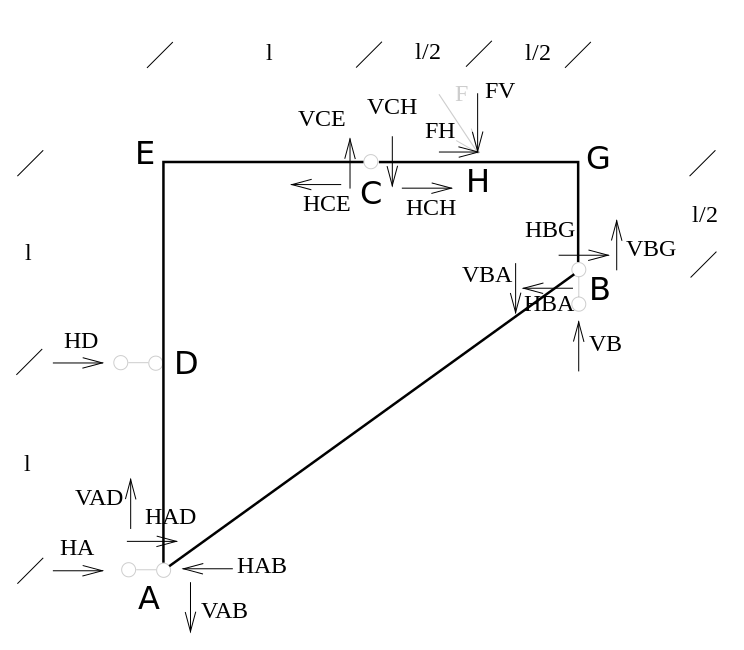
Una volta fatte queste sostituzioni, è necessario procedere all'analisi statica della struttura. Prima di tutto, conviene fare delle valutazioni sull'equilibrio dei nodi della struttura, i quali devono naturalmente essere equilibrati in quanto anch'essi parte della struttura stessa.

Analizziamo il nodo A:

Si fa notare che in corrispondenza del nodo le forze sono opposte a quelle che si dovranno considerare quando si andrà ad analizzare l'equilibrio delle aste. Per studiare l'equilibrio dei nodi, infatti, si deve immaginare di tagliare la struttura nell'intorno del nodo stesso. Le forze che il nodo e le aste in esso concorrenti si scambiano si presentano uguali ed opposte per il principio di azione e reazione. Osservando la figura, inoltre, si capisce che nel caso in cui le aste concorrenti siano due e non ci siano forze applicate in corrispondenza del nodo le azioni agenti su un'asta sono uguali e opposte a quelle agenti sull'altra.

Nel nostro caso particolare nel nodo è presente una cerniera interna, per cui le due porzioni di struttura non possono scambiarsi alcun momento flettente; è presente inoltre un vincolo esterno, che viene tenuto in conto per mezzo della sua reazione vincolare ancora incognita.

Il nodo, al contrario dell'asta, ha solo due gradi di libertà nel piano, per cui ci sono disponibili solo le due equazioni che forniscono le condizioni di equilibrio alla traslazione orizzontale e verticale:

${\begin{cases}H_{A}+H_{AB}-H_{AD}=0\\V_{AD}-V_{AB}=0\to V_{AD}=V_{AB}\end{cases}}$

Ugualmente per il nodo B:

${\begin{cases}H_{BA}-H_{BG}=0\to H_{BA}=H_{BG}\\V_{BA}+V_{B}-V_{BG}=0\end{cases}}$

Per il nodo C non sono necessarie particolari specificazione: visto che non esistono forze applicate si ha semplicemente:

${\begin{cases}H_{CE}=H_{CH}\\V_{CE}=V_{CH}\end{cases}}$

Valutiamo ora l'equilibrio dell'intera struttura.

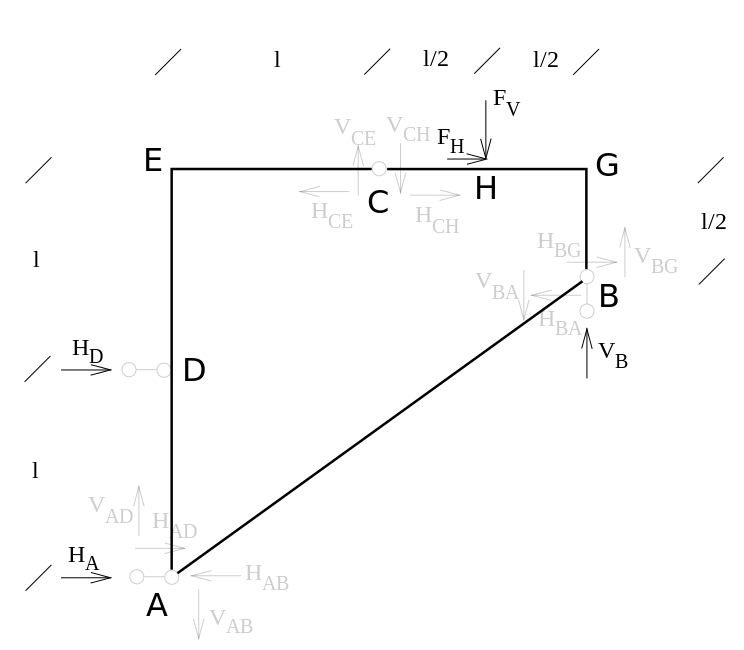
Eliminando in partenza i termini che è già noto essere uguali e opposti, si ha:

${\begin{cases}F_{V}-V_{B}=0\to V_{B}=F_{V}=4KN\\H_{D}+H_{A}+F_{H}=0\\V_{B}l/2+H_{D}l+H_{A}2l=0\end{cases}}$

Da cui si deduce:

${\begin{cases}V_{B}=4KN\\H_{D}=-4KN\\H_{A}=1KN\end{cases}}$

Consideriamo poi il tratto AEC:

${\begin{cases}H_{AD}+H_{D}-H_{CE}=0\\V_{AD}+V_{CE}=0\to V_{AD}=-V_{CE}\\H_{D}l-H_{CE}2l-V_{CE}l=0\end{cases}}$

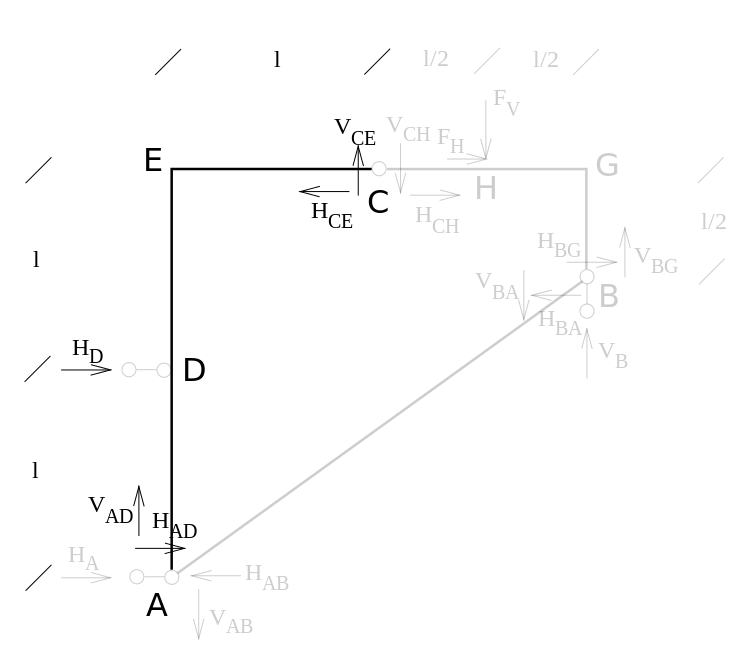
Per il tratto AB, poi, si ottiene:

${\begin{cases}H_{BA}+H_{AB}=0\to H_{BA}=-H_{AB}\\V_{BA}+V_{AB}=0\to V_{BA}=-V_{AB}\\H_{BA}{\frac {3l}{2}}-V_{BA}2l=0\to V_{BA}={\frac {3}{4}}H_{BA}\end{cases}}$

Considerare anche il tratto CGB è inutile dal momento che le relazioni che si otterrebbero sarebbero combinazioni lineari di quelle già ottenute. Conviene ora riportare tutte le equazioni finora trovate, in modo da facilitare la risoluzione:

${\begin{cases}H_{A}+H_{AB}-H_{AD}=0\\V_{AD}=V_{AB}\\H_{BA}=H_{BG}\\V_{BA}+V_{B}-V_{BG}=0\\H_{CE}=H_{CH}\\V_{CE}=V_{CH}\\V_{B}=4KN\\H_{D}=-4KN\\H_{A}=1KN\\H_{AD}+H_{D}-H_{CE}=0\\V_{AD}=-V_{CE}\\H_{D}l-H_{CE}2l-V_{CE}l=0\\H_{BA}=-H_{AB}\\V_{BA}=-V_{AB}\\V_{BA}={\frac {3}{4}}H_{BA}\end{cases}}$

Risoluzione

Per risolvere questo sistema di ben 15 equazioni in altrettante incognite si può operare in molti modi differenti.

Si trasformino le equazioni precedenti in modo da averle nella forma $X=aY+bZ+...$, dove $X,Y,Z$ rappresentano le incognite delle equazioni e $a,b$ dei coefficienti.

${\begin{cases}H_{AB}=-H_{A}+H_{AD}\\V_{AD}=V_{AB}\\H_{BA}=H_{BG}\\V_{BG}=V_{BA}+V_{B}\\H_{CE}=H_{CH}\\V_{CE}=V_{CH}\\V_{B}=4KN\\H_{D}=-4KN\\H_{A}=1KN\\H_{AD}=-H_{D}+H_{CE}\\V_{AD}=-V_{CE}\\V_{CE}l=H_{D}l-H_{CE}2l\\H_{BA}=-H_{AB}\\V_{AB}=-V_{BA}\\V_{BA}={\frac {3}{4}}H_{BA}\end{cases}}$

Si sostituiscono, dunque, le espressioni trovate per ogni incognita ovunque essa compare:

${\begin{cases}H_{AB}=-H_{A}+H_{AD}=-1-H_{D}+H_{CE}=-1+4+H_{CH}=3+H_{CH}\\V_{AD}=V_{AB}=-V_{BA}=-{\frac {3}{4}}H_{BA}={\frac {3}{4}}H_{AB}={\frac {9}{4}}+{\frac {3}{4}}H_{CH}\\H_{BG}=H_{BA}=-H_{AB}=-3-H_{CH}\\V_{BG}=V_{BA}+V_{B}={\frac {3}{4}}H_{BA}+4=4-{\frac {3}{4}}H_{AB}=4-{\frac {9}{4}}-{\frac {3}{4}}H_{CH}\\H_{CE}=H_{CH}\\V_{CH}=V_{CE}=-V_{AD}=-{\frac {9}{4}}-{\frac {3}{4}}H_{CH}\\V_{B}=4KN\\H_{D}=-4KN\\H_{A}=1KN\\H_{AD}=-H_{D}+H_{CE}=4+H_{CH}\\V_{CE}=-V_{AD}=-{\frac {9}{4}}-{\frac {3}{4}}H_{CH}\\V_{CE}l=H_{D}l-H_{CE}2l\to V_{CE}=-4-2H_{CH}\\H_{BA}=-H_{AB}=-3-H_{CH}\\V_{AB}=-V_{BA}=-{\frac {3}{4}}H_{BA}={\frac {3}{4}}H_{AB}={\frac {9}{4}}+{\frac {3}{4}}H_{CH}\\V_{BA}={\frac {3}{4}}H_{BA}=-{\frac {3}{4}}H_{AB}=-{\frac {9}{4}}-{\frac {3}{4}}H_{CH}\end{cases}}$

Come si può osservare, in seguito a queste sostituzioni si è riusciti ad esprimere tutte le incognite in funzione esclusivamente di $H_{CH}$, che tuttavia non è ancora stata definita. Si osservino tuttavia le espressioni undicesima e dodicesima:

${\begin{cases}V_{CE}=-{\frac {9}{4}}-{\frac {3}{4}}H_{CH}\\V_{CE}=-4-2H_{CH}\\\end{cases}}$

Esse esprimono la medesima quantità $V_{CE}$, per cui i secondi termini delle due devono essere per forza di cose uguali:

$-{\frac {9}{4}}-{\frac {3}{4}}H_{CH}=-4-2H_{CH}\to H_{CH}=-{\frac {7}{5}}$

Sostituendo tale risultato nelle altre equazioni si ottengono tutti i valori delle incognite:

${\begin{cases}H_{AB}=3+H_{CH}=3-{\frac {7}{5}}={\frac {8}{5}}\\V_{AD}={\frac {9}{4}}+{\frac {3}{4}}H_{CH}={\frac {9}{4}}-{\frac {21}{20}}={\frac {6}{5}}\\H_{BG}=-3-H_{CH}=-3+{\frac {7}{5}}=-{\frac {8}{5}}\\V_{BG}=4-{\frac {9}{4}}-{\frac {3}{4}}H_{CH}={\frac {7}{4}}+{\frac {21}{20}}={\frac {14}{5}}\\H_{CE}=H_{CH}=-{\frac {7}{5}}\\V_{CH}=-{\frac {9}{4}}-{\frac {3}{4}}H_{CH}=-{\frac {6}{5}}\\V_{B}=4KN\\H_{D}=-4KN\\H_{A}=1KN\\H_{AD}=4+H_{CH}=4-{\frac {7}{5}}={\frac {13}{5}}\\V_{CE}=-{\frac {9}{4}}-{\frac {3}{4}}H_{CH}=-{\frac {6}{5}}\\H_{BA}=-3-H_{CH}=-{\frac {8}{5}}\\V_{AB}={\frac {9}{4}}+{\frac {3}{4}}H_{CH}={\frac {6}{5}}\\V_{BA}=-{\frac {9}{4}}-{\frac {3}{4}}H_{CH}=-{\frac {6}{5}}\\H_{CH}=-{\frac {7}{5}}\end{cases}}$