Classificazione dei triangoli (scuola media)

Classificazione dei triangoli (scuola media)
	Tipo: lezione
	Materia: Matematica per la scuola media 1
	Avanzamento: lezione completa al 50%.

Video per chi non ama leggere: Schooltoon, Il triangolo - Geometria - Secondaria di Primo Grado, su YouTube, 8 ott 2020.

Presi tre punti, non allineati, nel piano si possono congiungere con tre segmenti la figura ottenuta è un triangolo.

I triangoli^VK possono essere suddivisi a secondo delle relazioni tra i lati^VK oppure di quelle tra gli angoli^VK.

Si può fruire di questa lezione in forma di mappa mentale su wiki2map

In geometria il triangolo è un poligono con tre lati^VK, di conseguenza il triangolo ha tre vertici^VK e quindi tre angoli^VK. Il triangolo è la figura con il minor numero di lati, infatti non esistono poligoni^VK con due o un lato.

In un triangolo non si possono tracciare diagonali.

Classificazione attraverso i lati[modifica]

Video per chi non ama leggere: BB Prof, 50 I triangoli, su YouTube, 24 mag 2020.

Triangolo scaleno[modifica]

Il triangolo scaleno ha tre lati diversi.

Triangolo scaleno^VK
Triangolo scaleno
Triangolo scaleno^VK
Triangolo scaleno-rettangolo

Triangolo isoscele[modifica]

Ha due lati congruenti

Triangolo equilatero[modifica]

Ha tutti i tre lati congruenti

Classificazione attraverso gli angoli[modifica]

Triangolo ottusangolo[modifica]

Ha un angolo ottuso e due acuti.

Triangolo acutangolo[modifica]

Ha tutti gli angoli acuti.

Triangolo rettangolo[modifica]

Ha un angolo retto e due acuti. .

Esercizi per capire la classificazione dei triangoli[modifica]

Esercizi par imparare la classificazione dei triangoli[modifica]

Disegna un triangolo rettangolo e misura angoli e lati
Disegna un triangolo rettangolo appoggiato sul cateto maggiore con un angolo di 30°, misura l'altro angolo e tutti i lati
Disegna un triangolo con due angoli di misura 30° e 60°. Che triangolo è? Due dei lati sono in una particolare rapporto?
Disegna un triangolo isoscele
Disegna un triangolo con due angoli da 45°. Che triangolo è?

Tabella riassuntiva[modifica]

	Scaleno	Isoscele	Equilatero
Acutangolo	Tutti i lati diversi e tutti gli angoli acuti	Due lati congruenti e tre angoli acuti	Tutti i lati congruenti e tre angoli acuti
Rettangolo	Tutti i lati diversi e un angolo retto e due acuti	Due lati congruenti e un angolo retto e due acuti	Non esiste
Ottusangolo	Tutti i lati diversi e un angolo ottuso e due acuti	Due lati congruenti e un angolo ottuso e due acuti	Non esiste

La somma degli angoli di un triangolo[modifica]

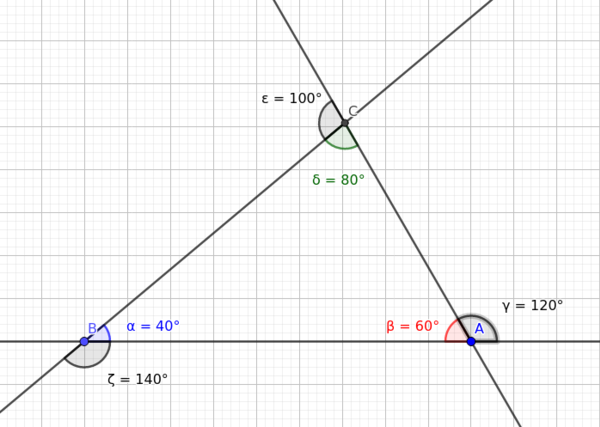
Ricordando le proprietà delle parallele tagliate da una trasversale^VK è possibile comprendere che la somma degli angoli interni di un triangolo è uguale a 180° gradi.

- La formula per calcolare gli angoli interni è $180^{\circ }\times [n-2]=180^{\circ }\times [3-2]=180^{\circ }\times 1=180^{\circ }$ .

- La somma degli angoli esterni è per tutti i poligoni 360°.

Costruire un triangolo[modifica]

Per disegnare un triangolo date le misure dei lati si procede con riga e compasso, disegno che ovviamente può servire da modello per la costruzioni di triangoli anche reali e di materiali diversi.

Nell'ipotesi che si voglia disegnare un triangolo di lati 7cm, 5cm e 4cm, si procede come segue.

Segmento^VK
Disegnato il segmento che sarà la base (7cm)
Circonferenza^VK
Puntando su un estremo si disegna una circonferenza
di raggio uguale al secondo lato (5cm)
Circonferenza^VK
Dal secondo estremo si traccia una circonferenza
di raggio pari al terzo lato (4cm)
Vertice^VK
Il punto di intersezione delle circonferenze
è il terzo vertice del triangolo (C)
Triangolo^VK
Congiungendo i tre punti si ottiene il triangolo
Triangolo^VK
Triangolo con in evidenza le misure dei lati
(AB = 7cm, AC = 5cm e BC = 4cm)

Riassumendo in una lista come nelle immagini:

Disegnato il segmento che sarà la base (AB = 7cm)
Puntando su un estremo si disegna una circonferenza di raggio uguale al secondo lato (5cm)
Dal secondo estremo si traccia una circonferenza di raggio pari al terzo lato (4cm)
Il punto di intersezione delle circonferenze è il terzo vertice del triangolo (C)
Congiungendo i tre punti si ottiene il triangolo
Triangolo con in evidenza le misure dei lati (AB = 7cm, AC = 5cm e BC = 4cm)

Condizioni di costruibilità[modifica]

In questa immagine vediamo che dati due lati, nell'esempio di misura 7cm e 4cm, è possibile costruire triangoli con un terzo lato di misura compresa tra 3 cm e 11 cm.

Sono disegnati triangoli con lati :

7cm, 4cm e 5cm;
7cm, 4cm e 6cm;
7cm, 4cm e 10cm;

e persino i triangoli degeneri

7cm, 4cm e 3cm
7cm, 4cm e 11cm

che di fatto sono segmenti.

E' evidente come non sia possibile costruire un triangolo con i lati di 7 cm, 4 cm e 2 cm, le circonferenze non si intersecano quindi non trovo il terzo vertice.

La non costruibilità di un triangolo con i lati di 7 cm, 4 cm e 2 cm, non dipende dalle scelte costruttive, anche partendo dal lato di 2 cm...

Disegnare un triangolo isoscele[modifica]

Per disegnare un triangolo isoscele qualsiasi si possono seguire due metodi:

una volta scelto il segmento di base si traccia il suo asse e su questo si sceglie un punto che diventa il vertice del triangolo, e lo si congiunge con gli estremi della base
disegnata una circonferenza si tracciano due raggi che diventano i lati obliqui il segmento che si ottiene congiungendo gli estremi dei raggi sulla circonferenza è la base

Nella immagini che seguono viene disegnato un triangolo isoscele di lati 4cm e con un angolo al vertice di 80°.

Circonferenza^VK
Si disegna una circonferenza
di raggio pari alla misura dei lati obliqui
( $r=4cm$ )
Retta^VK
Si sceglie un punto sulla circonferenza,
e si disegna l'angolo al vertice nel centro
( $\alpha =80^{\circ }$ )
Angolo^VK
Si traccia il triangolo congiungendo il primo punto scelto
con il centro e con quello ottenuto
disegnando l'angolo
$ABB'$
Vertice^VK
Il triangolo ottenuto con le misure in evidenza

Si disegna una circonferenza di raggio pari alla misura dei lati obliqui
Si sceglie un punto sulla circonferenza, e si disegna l'angolo al vertice nel centro
Si traccia il triangolo congiungendo il primo punto scelto con il centro e con quello ottenuto disegnando l'angolo

Proprietà dei lati del triangolo[modifica]

Punti notevoli[modifica]

Ortocentro: punto d'intersezione delle altezze.

Baricentro: punto d'intersezione delle mediane.

Incentro: punto d'intersezione delle bisettrici.

Circocentro: punto d'intersezione delle assi.

Criteri di congruenza[modifica]

1) Criterio di congruenza su i triangoli Se due triangoli hanno rispettivamente due lati congruenti e l'angolo tra essi compreso,essi sono congruenti.

2) Criterio di congruenza su i triangoli Se due triangoli hanno rispettivamente due angoli congruenti e il lato ad essi adiacente, essi sono congruenti.

3) Criterio di congruenza su i triangoli Se due triangoli hanno rispettivamente tre lati congruenti,essi sono congruenti.

Bibliografia[modifica]

Contaci Zanichelli, autori: Clara Bertinetto, Arja Metiainen, Johannes Paasonen, Eija Voutilainen

Quiz[modifica]

	due lati uguali
	un lato molto lungo
	tre lati uguali
	un angolo retto

	due lati uguali
	un lato molto lungo
	tre lati uguali
	un angolo retto

	due angoli uguali
	un angolo molto grande
	tre diversi
	due angoli retti

	due lati uguali
	i lati diversi
	tre lati uguali
	un angolo retto

	tre angoli retti
	due angoli retti
	un angolo retto
	poca intelligenza