Algoritmi (superiori)
Algoritmi
[modifica]Un algoritmo e' la tecnica/procedimento utilizzato per risolvere una specifica classe di problemi ad esempio :
l'ordinamento di un vettore (BubbleSort, QuickSort), la ricerca di un elemento in un vettore ordinato (ricerca binaria o dicotomica), indicizzazione/ricerca dati presenti nei siti web ( motore di ricerca di Google), compressione dei file musicali (mp3, flac, ...), compressione immagini( gif, jpeg, ....) crittografia a chiave asimmetrica (Algoritmo di Diffie-Hellman, Algoritmo RSA (Rivest-Shamir-Adleman)), compressione filmati (divx, avi, ...), ricerca percorso minimo di un grafo (Algoritmo di Dijkstra).
Un algoritmo nell'ambito informatico e' un codice che risolve con efficienza un particolare problema, per un matematico la definizione di algoritmo e' mirata a garantire l'effettiva computabilità del metodo
un algoritmo e' una sequenza ordinata e finita di istruzioni elementari che eseguita permette di ottenere un determinato risultato in un tempo finito .
La "bellezza" di un algoritmo spesso e' legata ai soli tempi di elaborazione cioe' a quanto velocemente riesce a risolvere un certo problema , in altri casi alla scelta della struttura dati utilizzata per formalizzare il problema (scelta del modello) e alla eleganza logica della tecnica risolutiva (chiarezza del codice e compattezza dello stesso).
Il termine algoritmo deriva dalla latinizzazione del nome del matematico persiano Al-Khwārizmī che scrisse un libro sulle regole per il calcolo aritmetico usando il sistema di numerazione indiano-arabo nel 12° secolo.
 |
 |
Vediamo un semplice algoritmo che permette di ordinare gli elementi di un vettore :
Per ordinare gli elementi di un vettore dal più piccolo al più grande si possono usare diversi algoritmi, quello più semplice da spiegare e' il BubbleSort e quello più veloce e' il QuickSort. Un algoritmo e' un particolare programma che risolve una classe di problemi (nel nostro caso l'ordinamento degli elementi di un vettore) con una certa efficienza ( generalmente espressa in termini di velocità di calcolo).
Bubblesort
[modifica]Per ordinare un vettore di n elementi bisogna fare n-1 passate, ad ogni passata l'elemento più piccolo rimasto nella parte di vettore ancora da ordinare viene spostato nella posizione corretta, per ordinare il vettore bastano n-1 passate perche' sistemati i primi n-1 elementi anche l'ultimo numero e' per forza di cose al posto giusto. In una singola passata , pensiamo sia la passata i-esima si prendono in considerazione tutti gli elementi partendo dall'ultimo (indice n-1) fino a quello con l'indice con lo stesso numero della passata, ogni elemento considerato ad esempio quello k-esimo viene confrontato con quello che lo precede k-1-esimo e se vett[k] < vett[k-1] i due elementi del vettore si scambiano fra loro , altrimenti si passa a considerare l'elemento successivo. Facciamo un esempio , vettore di 6 elementi , passate da fare 5, nella prima passata si ha
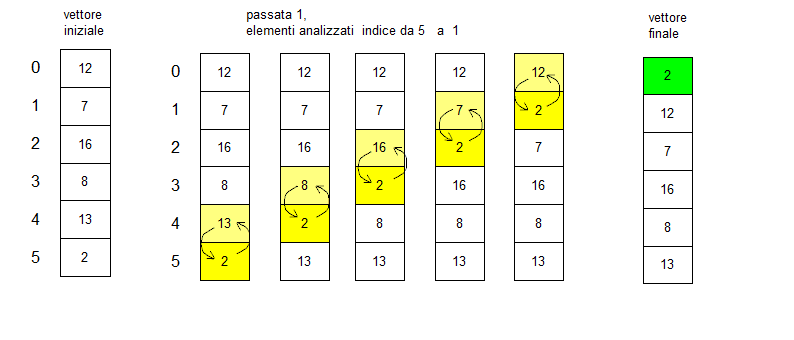
come si vede, alla fine della prima passata il vettore e' composto da due parti una ordinata (colore verde) che contiene il numero più piccolo (2) e una che deve essere ancora ordinata, la seconda passata si occupa di ordinare soltanto di quest'ultima, si vede che per fare la prima passata bisogna considerare via via gli elementi in giallo con il corrispondente elemento che lo precede, sono queste coppie di valori che vengono confrontate ed eventualmente scambiate fra loro.
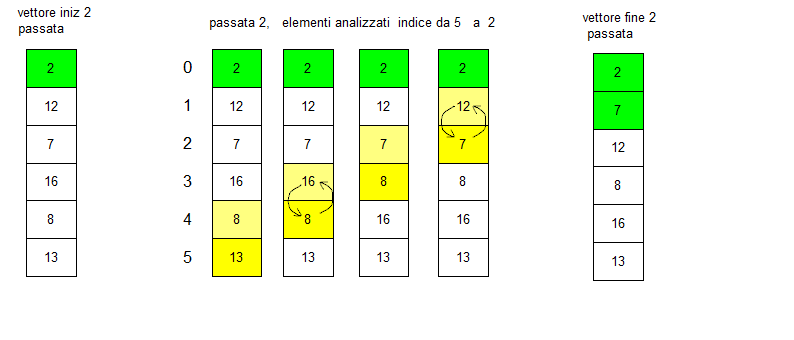
Nella seconda passata si ha:
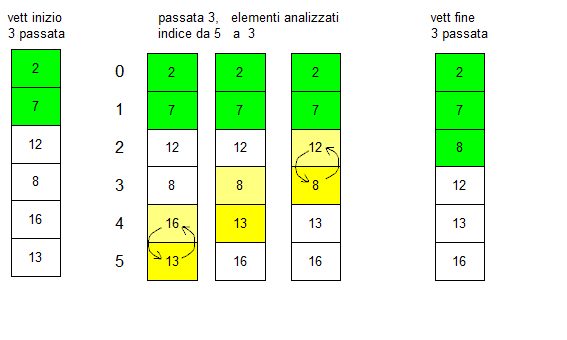
il vettore ordinato e' composto ora da due numeri e il vettore da ordinare e' diventato più piccolo, si nota che il numero di confronti che si devono fare si riduce di conseguenza di una unità ad ogni passata.Vediamo la passata 3
Vediamo la passata 4
vediamo la passata 5
si nota che durante la passata 4 non ci sono stati scambi , quando non ci sono scambi durante tutta una passata il vettore risulta ordinato e ele passate successive non sono più necessarie, in questa spiegazione e nel programma seguente non utilizzeremo questa particolarità che consente di velocizzare la fine dell'algoritmo.
Il programma e' caratterizzato da un primo ciclo for che conta le passate ( conta da 1 ) e all'interno della singola passata c'e un secondo for che prende in analisi i diversi elementi J (partendo dal fondo n-1 fino a quello di indice pari al numero della passata) che devono essere confrontati con l'elemento del vettore che lo precede J-1 , si nota poi la necessità dell'uso della variabile temp per poter scambiare due celle di un vettore senza perdersi uno dei valori delle celle.
In questo programma l'ordinamento e' fatto su un vettore di stringhe (parole), in questo caso l'ordinamento e' quello alfabetico (antonella minore di zorro)
BubbleSort
#include <cstdlib>
#include <iostream>
#include <string>
using namespace std;
/* dato un vettore disordinato ordinarlo con il bubblesort
e poi stamparlo
*/
int main(int argc, char *argv[])
{
int n=5;
string vett[5];
int i,j;
string temp;
for (i=0;i<n;i++)
{ cout<<"inserisci il "<<i<<" elemento ";
cin>>vett[i];
}
cout<<"stampa vettore disordinato"<<endl;
for (i=0;i<n;i++)
{ cout<<vett[i]<<" , ";
}
cout<<endl;
//Bubblesort
for (i=1;i<n;i++)
for ( j= n-1;j>=i;j--)
if(vett[j]<vett[j-1])
{ temp= vett[j];
vett[j]=vett[j-1];
vett[j-1]=temp;
}
cout<<"stampa vettore ordinato"<<endl;
for (i=0;i<n;i++)
{ cout<<vett[i]<<" , ";
}
cout<<endl;
system("PAUSE");
return 0;
}
In Octave
v=[3 1 5 23 67 0 78 -4 88 23 ]
n=10;
for i=2:n
for j= n:-1:i
if (v(j)<v(j-1))
temp=v(j);
v(j)=v(j-1);
v(j-1)=temp;
endif
endfor
endfor
v
L'efficienza di un algoritmo viene espressa con l'ordine di complessità, generalmente esso dipende dal numero n di elementi del vettore, se le operazioni da fare per completare l'algoritmo fossero proporzionali al numero di elementi del vettore l'odine di complessità sarebbe indicato come e si legge O grande di n. Nel caso del bubblesort le cose vanno peggio di O(n) e i calcoli da farsi sono proporzionalia a secondo un fattore di proporzionalità di 0.5 si ha allora . Per il quicksort l'ordine di complessità e' del , meglio del bubblesort ma peggio di un andamento solamente proporzionale ad n . Vediamo in un grafico l'andamento delle istruzioni da effettuare in 3 casi diversi di complessità