Teoria generale della scelta e delle preferenze

Obiettivi della lezione

• Presentazione della modellizzazione delle preferenze dei consumatori
• Comprendere il collegamento che c'è tra preferenze e funzione di utilità e le assunzione che questo richiede
• Proprietà delle funzioni di utilità

Modellizzazione delle preferenze

Sia $X\subseteq \mathbb {R} _{+}^{n}$, l'insieme di consumo, dove $n\in \mathbb {N}$ è il numero di beni disponibili. I vettori $\mathbf {x} \in X$, di dimensione $n$, sono i possibili panieri di consumo a disposizione dei consumatori, ed i loro elementi, $x_{l}\in \mathbb {R} _{+}$, sono la quantità di bene $l\in \mathbb {N}$ consumata.

• In questo tipo di formalizzazione matematica stiamo implicitamente assumendo che tutti i beni siano perfettamente divisibili, infatti le quantità appartengono all'insieme dei reali.
• Altra questione è la definizione di bene: come facciamo a distinguere un bene dall'altro? Il "cellulare" è un bene? O bisogna indetificare la marca? E il colore? E il luogo d'acquisto? E il tempo in cui il bene è disponibile? Gli stati di natura (pioggia o sole, ad esempio)? In pratica, a seconda dell'applicazione che si sta facendo del modello, sarà necessario stabilire il livello di aggregazione dei beni.

Sia $\succcurlyeq$ una Relazione binaria definita come: $\mathbf {x} \succcurlyeq \mathbf {y}$ se $\mathbf {x}$ è debolmente preferito a (o "almento tanto buono quanto") $\mathbf {y}$.

Definiamo inoltre la preferenza stretta: $\mathbf {x} \succ \mathbf {y} \Leftrightarrow \mathbf {x} \succcurlyeq \mathbf {y} \land \mathbf {y} \not \succcurlyeq \mathbf {x}$ e l'indifferenza: $\mathbf {x} \sim \mathbf {y} \Leftrightarrow \mathbf {x} \succcurlyeq \mathbf {y} \land \mathbf {y} \succcurlyeq \mathbf {x}$

Finora non abbiamo fatto alcuna assunzione sulla struttura delle preferenze, a parte la perfetta divisibilità dei beni. Quello che abbiamo ottenuto è un modo di rappresentare le preferenze del generico consumatore: questo metodo di rappresentazione, però, non è molto maneggevole dal punto di vista matematico. Quello che invece risulterebbe comodo avere è una funzione di utilità tale che: $\mathbf {x} \succcurlyeq \mathbf {y} \Leftrightarrow u\left(\mathbf {x} \right)\geq u\left(\mathbf {y} \right)$ dove $u\left(\mathbf {x} \right):X\rightarrow \mathbb {R}$

In sostanza tale funzione di utilità assegna a ciascun paniere un numero in modo tale che un paniere, $\mathbf {x}$, è debolmente preferito ad un altro, $\mathbf {y}$, se e solo se il numero associato al primo è maggiore o uguale al numero associato al secondo.

Passiamo ora a vedere quali sono le assunzioni necessarie al fine di ottenere una funzione di utilità.

Ipotesi imposte sulle preferenze

Completezza

$\forall \mathbf {x} ,\mathbf {y} \in X:\mathbf {x} \succcurlyeq \mathbf {y} \lor \mathbf {y} \succcurlyeq \mathbf {x}$

Ossia: presi due qualsiasi panieri di consumo almeno uno dei due è debolmente preferito all'altro. Ciò significa che due qualunque panieri sono sempre confrontabili tra loro: in sostanza viene richiesto al consumatore di essere sempre in grado di decidere, eventualmente esprimendo l'indifferenza (doppia preferenza debole), ma mai rifiutandosi di rispondere.

Riflessività

$\forall \mathbf {x} \in X:\mathbf {x} \succcurlyeq \mathbf {x}$

Ossia: qualunque paniere di consumo è debolmente preferito a se stesso. Tale proprietà può essere considerata ridondante, data l'ipotesi di completezza delle preferenze, tuttavia vale la pena di specificarla espressamente.

Transitività

$\forall \mathbf {x} ,\mathbf {y} ,\mathbf {z} \in X:\mathbf {x} \succcurlyeq \mathbf {y} \land \mathbf {y} \succcurlyeq \mathbf {z} \Rightarrow \mathbf {x} \succcurlyeq \mathbf {z}$

Ossia: dati tre qualsiasi panieri di consumo, se il primo è debolmente preferito al secondo, e il secondo al terzo, allora anche il primo paniere è debolmente preferito al terzo.

• Data tale proprietà, è possibile dimostrare che anche $\succ$ e $\sim$ sono transitive (la dimostrazione è lasciata come esercizio). Sulla transitività di tali relazioni è possibile menzionare diversi paradossi, in particolare il paradosso di Condorcet, che però riguarda le preferenze collettive; per quanto riguarda, invece, la transitività dell'indifferenza, si presuppone che il consumatore sia in grado di distinguere beni aventi differenze infinitesime.
• Si noti, a questo punto, che la preferenza debole, date le proprietà di riflessività e transitività, è un preordine; inoltre la relazione di indifferenza è riflessiva, simmetrica e transitiva, dunque è una relazione di equivalenza. Tale relazione determina, quindi, una partizione dell'insieme di consumo con suddivisione in classi di equivalenza. L'insieme quoziente $X/\sim$ risulta, dunque, totalmente ordinato mediante la $\succ$.

Continuità

$\forall \mathbf {y} \in X$, $\left\{\mathbf {x} \in X|\mathbf {x} \succcurlyeq \mathbf {y} \right\}$ e $\left\{\mathbf {x} \in X|\mathbf {y} \succcurlyeq \mathbf {x} \right\}$ sono insiemi chiusi

Questo significa che, data una successione di panieri $\mathbf {x} _{n}$ che convergono ad un paniere $\mathbf {x}$, se $\mathbf {y}$ è preferito a tutti i panieri della successione, è anche preferito a $\mathbf {x}$, e viceversa.

Questa proprietà permette di escludere alcuni tipi di preferenza, come l'ordine lessicografico; in quest'ultimo caso, infatti, esisterebbe un bene che non è sostituibile con gli altri e non verrebbe mai scambiato.

Monotonicità forte

$\forall \mathbf {x} \neq \mathbf {y} ,x_{l}\geq y_{l}\forall l\Rightarrow \mathbf {x} \succ \mathbf {y}$

Ossia: presi due qualsiasi panieri distinti, se uno dei due ha almeno la stessa quantità di ciascun bene rispetto all'altro, allora gli risulta strettamente preferito. In altre parole, se due panieri sono identici, ma uno dei due ha almeno per un bene una quantità strettamente maggiore, allora deve risultare strettamente preferito.

• Nella definizione di monotonicità debole si sostituisce la preferenza stretta con quella debole.
• L'assunzione di monotonicità forte contrasta con le preferenze alla Leontief.

Teorema di rappresentazione di Debreu

Se le preferenze $\succcurlyeq$, definite su $X=\mathbb {R} _{+}^{n}$, sono (riflessive,) complete, transitive, continue e strettamente monotoniche, allora esiste una funzione $u:X\rightarrow \mathbb {R}$ tale che: $\forall \mathbf {x} ,\mathbf {y} \in X,u\left(\mathbf {x} \right)\geq u\left(\mathbf {y} \right)\Leftrightarrow \mathbf {x} \succcurlyeq \mathbf {y}$

Dimostriamo solo l'esistenza della funzione; per la continuità si rinvia all'articolo originale di Debreu (1954). Sia $\mathbf {e}$, vettore in $\mathbb {R} _{+}^{n}$, costituito da tutti uno. Dato qualsiasi paniere $\mathbf {x} \in X$, sia $u\left(\mathbf {x} \right)$ il numero tale che $\mathbf {x} \sim u\left(\mathbf {x} \right)\mathbf {e}$, ossia tale che il paniere dato è indifferente ad un paniere costituito dalla quantità $u\left(\mathbf {x} \right)$ di ciascun bene. Dimostriamo che tale numero esiste per ogni $\mathbf {x} \in X$ ed è unico:

• sia $B\equiv \left\{t\in \mathbb {R} |t\mathbf {e} \succcurlyeq \mathbf {x} \right\}$ l'insieme di tutti i numeri reali tali che i panieri costituiti da una tale quantità di ciascun bene sono debolmente preferiti a $\mathbf {x}$; tale insieme è non vuoto, visto che almeno contiene tutti i $t$ maggiori della più grande quantità di bene contenuta in $\mathbf {x}$: infatti, data la monotonicità imposta alle preferenze, $t\mathbf {e}$ è sicuramente preferito a $\mathbf {x}$.
• sia $W\equiv \left\{t\in \mathbb {R} |\mathbf {x} \succcurlyeq t\mathbf {e} \right\}$ l'insieme di tutti i numeri reali tali che $\mathbf {x}$ è preferito ai panieri costituiti da una tale quantità di ciascun bene; anche tale insieme non è vuoto, visto che almento contiene lo zero.
• $B$ e $W$ sono entrambi chiusi, dato l'assioma di continuità.
• per l'assioma di completezza, tutti i panieri sono confrontabili, dunque $B\cup W=\mathbb {R}$.
• viste le due osservazioni precedenti, $B\cap W\neq \emptyset$, in quanto devono almeno avere il punto di frontiera in comune; a questo punto ci si chiede se l'intersezione è un singolo punto (solo in tal caso potremmo parlare di funzione):
  • per assurdo, si assuma l'esistenza di $t>t'|t,t'\in B\cup W$, si avrebbe $t'\mathbf {e} \sim \mathbf {x} \sim t\mathbf {e}$ e, per la transitività, $t'\mathbf {e} \sim t\mathbf {e}$, in contrasto con $t\mathbf {e} \succ t'\mathbf {e}$, implicata dalla monotonicità stretta. Quindi l'intersezione è un singleton.

Una volta dimostrata l'esistenza e l'unicità di tale numero, rimane da dimostrare che $\forall \mathbf {x} ,\mathbf {y} \in X,u\left(\mathbf {x} \right)\geq u\left(\mathbf {y} \right)\Leftrightarrow \mathbf {x} \succcurlyeq \mathbf {y}$, ossia che la funzione "funzioni" in modo corretto. La dimostrazione è banale e si basa sulla monotonicità stretta e la transitività, dunque la si riporta in simboli senza commenti:

• $\Rightarrow$ - per la monotonicità stretta: $u\left(\mathbf {x} \right)>u\left(\mathbf {y} \right)\Rightarrow u\left(\mathbf {x} \right)\mathbf {e} \succ u\left(\mathbf {y} \right)\mathbf {e}$ e per la transitività $\mathbf {x} \succ \mathbf {y}$
• $\Leftarrow$ - è uguale alla precedente

Illustrazione del teorema di Debreu in 2 variabili

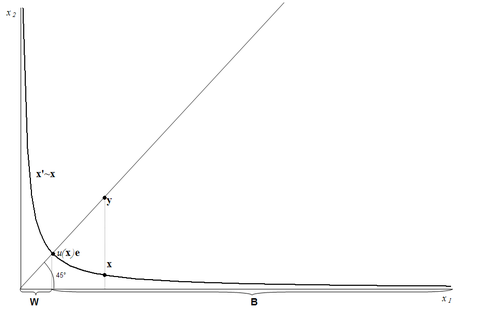
Volendo rappresentare il problema su due dimensioni, si immagini di avere il generico paniere $\mathbf {x}$. Tutti i panieri sono confrontabili con $\mathbf {x}$, ed in particolare quelli che si trovano sulla prima bisettrice. Questi ultimi sono tutti non indifferenti tra loro, per via della stretta monotonicità: sono, anzi, perfettamente ordinabili mediante la preferenza stretta. Visto che esiste almeno un paniere come $\mathbf {y}$ (strettamente preferito a $\mathbf {x}$) ed almeno un paniere non preferito a $\mathbf {x}$ (l'origine), per via della continuità siamo certi dell'esistenza del paniere $u\left(\mathbf {x} \right)\mathbf {e} \sim \mathbf {x}$,e , sempre per la stretta monotonicità, questo è unico.

Dal grafico, inoltre, è possibile catturare l'idea di classe d'equivalenza in questo contesto. Ogni paniere appartiene ad una classe di equivalenza (che costituiscono le curve di indifferenza, che vedremo più avanti), il cui elemento rappresentativo potrebbe essere uno dei panieri sulla bisettrice. Lo spazio di tutti i panieri $X$ è partizionato in curve di indifferenza, e l'insieme di tali infinite curve è l'insieme quoziente $X/\sim$, il quale è totalmente ordinato mediante la preferenza stretta, come facilmente si comprende osservando i panieri rappresentativi sulla bisettrice: questi sono, infatti, totalmente ordinati per via della monotonicità stretta delle preferenze.

Proprietà delle funzioni di utilità

• Ogni funzione di utilità è unica a meno di una trasformazione monotonica crescente, ovvero applicando una arbitraria funzione monotona crescente alla funzione di utilità, otteniamo tutte le possibili funzioni di utilità rappresentative delle preferenze date. Si dice, quindi, che l'utilità ha natura ordinale: il valore assunto dalla funzione di utilità per un determinato paniere non ha significato in se, quello che conta è l'ordine. Se, ad esempio, un paniere ha utilità 100 ed un altro 10, possiamo solo concludere che il primo è preferito al secondo, non che il primo è 10 volte più utile del secondo.
• Si definisce curva d'indifferenza, o di isoutilità, l'insieme di tutti i panieri aventi la stessa utilità. È, dunque, chiaro il parallelo con le classi di equivalenza di cui si è parlato in precedenza. Volendo ottenere l'equazione della generica curva d'indifferenza, nel caso di due soli beni, in modo da poterne tracciare il grafico, bisogna seguire lo stesso procedimento utilizzato per disegnare le curve di livello di una funzione, ossia:
  • Data la funzione di utilità $u\left(x_{1},x_{2}\right)$, si considerino le combinazioni dei due beni aventi la stessa utilità: $u\left(x_{1},x_{2}\right)=k$
  • Si imponga che il differenziale totale sia nullo (l'utilità, date le variazioni di $x_{1},x_{2}$, rimane costante): $du={\frac {\partial u\left(x_{1},x_{2}\right)}{\partial x_{1}}}dx_{1}+{\frac {\partial u\left(x_{1},x_{2}\right)}{\partial x_{2}}}dx_{2}=0$
  • Quindi si ottiene l'inclinazione della curva d'indifferenza: ${\frac {dx_{2}}{dx_{1}}}{\bigg |}_{du=0}=-{\frac {\frac {\partial u\left(x_{1},x_{2}\right)}{\partial x_{1}}}{\frac {\partial u\left(x_{1},x_{2}\right)}{\partial x_{2}}}}$; il valore assoluto di tale inclinazione viene detta saggio marginale di sostituzione tra $x_{1}$ e $x_{2}$, che indica di quanto deve aumentare la quantità di $x_{2}$ al diminuire della quantità di $x_{1}$ presente nel paniere, affinché il consumatore rimanga indifferente. In generale è $|SMS_{i,j}|={\frac {\frac {\partial u\left(\mathbf {x} \right)}{\partial x_{i}}}{\frac {\partial u\left(\mathbf {x} \right)}{\partial x_{j}}}}$
• Le curve di indifferenza hanno sempre inclinazione negativa: la monotonicità stretta esclude la possibilità di tratti ad inclinazione non negativa
• Per quanto visto in precedenza (le curve di indifferenza sono classi di equivalenza), per ogni paniere passa una ed una sula curva di indifferenza (ossia, due curve di indifferenza non si incrociano mai)
• Si assume che le preferenze siano convesse, ossia: $\forall \mathbf {x} ,\mathbf {y} ,\mathbf {z} \in X,\mathbf {x} \succcurlyeq \mathbf {z} \land \mathbf {y} \succcurlyeq \mathbf {z} \Rightarrow \lambda \mathbf {x} +\left(1-\lambda \right)\mathbf {y} \succcurlyeq \mathbf {z} ,\forall \lambda \in \left[0,1\right]$. Ciò significa che se due panieri sono debolmente preferiti ad un paniere dato, anche una loro combinazione è debolmente preferita al paniere dato. L'implicazione economica è che un paniere "medio" è debolmente preferito ai panieri estremi.
  • La convessità delle preferenze implica che le curve di indifferenza sono convesse, che il saggio marginale di sostituzione è decrescente e che la funzione di utilità è quasi-concava, ossia: $u\left[\lambda \mathbf {x} +\left(1-\lambda \right)\mathbf {y} \right]\geq \max \left[u\left(\mathbf {x} \right),u\left(\mathbf {y} \right)\right],\forall \lambda \in \left[0,1\right]$
• Nonostante si possano ottenere infinite funzioni di utilità, mediante una trasformazione monotonica crescente, il saggio marginale di sostituzione risulta invariante alle suddette trasformazioni.

Esercizi

1. Dato $X=\left\{\left(0,0\right),\left(1,0\right),\left(0,1\right),\left(1,1\right)\right\}$, l'insieme di consumo, dove nel generico paniere il primo numero indica il consumo di bene $x_{1}$ e il secondo il consumo di bene $x_{2}$.
   • Date le preferenze $\left(1,1\right)\succcurlyeq \left(0,0\right);\left(1,1\right)\succcurlyeq \left(1,0\right);\left(1,1\right)\succcurlyeq \left(0,1\right);\left(1,0\right)\succcurlyeq \left(0,1\right);\left(1,0\right)\succcurlyeq \left(0,0\right)$, si indichi quali assiomi non vengono rispettati.
   • Si scriva un esempio possibile di preferenze che rispetti tutti gli assiomi
2. Si dimostri che il saggio marginale di sostituzione è invariante a trasformazioni monotoniche crescenti di $u$
3. Si calcoli il saggio marginale di sostituzione delle seguenti funzioni di utilità e si traccino le curve di indifferenze nel caso di due soli beni:
   • $u\left(\mathbf {x} \right)=\prod _{i=1}^{N}x_{i}^{\alpha _{i}}$ (Utilità Cobb-Douglas)
   • $u\left(\mathbf {x} \right)=\sum _{i=1}^{N}\alpha _{i}x_{i}$ (Beni perfetti sostituti)
   • $u\left(\mathbf {x} \right)=\min \left[\left\{x_{i}\right\}_{i=1}^{N}\right]$ (Beni perfetti complementi)

Bibliografia

• G. Debreu. Representation of a Preference Ordering by a Numerical Function, in Thrall, Davis and Coombs Decision Processes. New York, John Wiley, 1954. pp. 159-165.
• T. Rader. The Existence of a Utility Function to Represent Preferences, «The Review of Economic Studies», 30, 1963, 3, 229-232.