Automa a stati finiti
| Lezione precedente: Introduzione allo studio dell'informatica teorica | Corso: Materia:Informatica Teorica | Prossima lezione: Teoremi sugli automi a stati finiti |
Introduzione e cenni storici
[modifica]Gli automi a stati finiti sono modelli matematici impiegati per la rappresentazione astratta della computazione; si veda a tal proposito, l'impostazione data da Dino Mandrioli nell'introduzione al capitolo sugli automi [1].
Panoramica storica
[modifica]Storicamente gli automi a stati finiti sono stati introdotti in modo poco formalizzato da Warren McCulloch e Walter Pitts in un articolo del 1943 che diede vita, tra le altre cose, allo studio delle reti neurali artificiali[2].
Successivamente David A. Huffman riprese e sviluppò il concetto di automa a stati finiti contestualizzandolo nell'ambito della progettazione di circuiti digitali[3].
Le idee di Huffman vennero ulteriormente perfezionate da George H. Mealy, che pubblicò il suo lavoro in un articolo [4] diventato un caposaldo in diversi settori dell'elettronica e dell'informatica.
Infine, Edward F. Moore propose un formalismo alternativo a quello di Mealy divenuto comunque prezioso nello sviluppo dei sistemi digitali [5].
Principio di funzionamento dell'automa
[modifica]Gli automi a stati finiti che studieremo nel nostro corso sono a tutti gli effetti delle macchine di Mealy, facilmente riconoscibili da due fattori: l'evoluzione dello stato dipende sia dallo stato attuale sia dall'ingresso dell'automa, inoltre l'uscita avviene durante le transizioni.
Più precisamente ogni automa a stati finiti può essere pensato come una macchina dotata di una testina per leggere i simboli scritti su un nastro ed un corpo principale che modifica il suo stato in funzione dei simboli letti. L'immagine sottostante mostra una versione stilizzata di tale dispositivo.
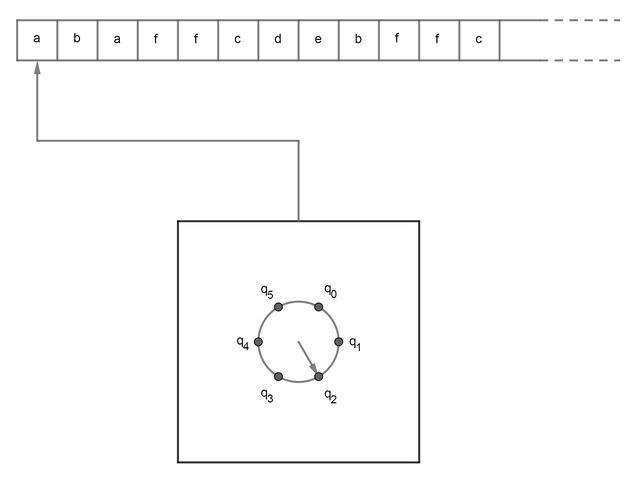
Idealmente, la sequenza di simboli in ingresso si trova codificata su un nastro che ha un punto iniziale ma che è virtualmente infinito: non c'è un limite massimo al numero di simboli che la macchina può leggere. Inoltre la lettura del nastro avviene sequenzialmente da sinistra verso destra; la testina non può muoversi nella direzione opposta.
L'automa è dotato di un ciclo di lavoro che viene ripetuto una volta per ogni simbolo di ingresso incontrato. Il ciclo di lavoro dell'automa a stati è molto semplice ed è composto da soli due passi:
- lettura dell'ingresso;
- evoluzione dello stato interno.
Nella fase di lettura dell'ingresso una testina legge dal nastro il simbolo che va elaborato, poi si sposta sulla posizione del simbolo successivo.
Nella fase di evoluzione l'automa adatta il proprio stato in accordo con il simbolo ricevuto in ingresso, considerando anche lo stato attuale; il cambiamento dello stato prende il nome di transizione.
Analogie con i calcolatori
[modifica]La breve descrizione appena presentata permette di sviluppare un parallelo tra la struttura dell'automa a stati finiti e la struttura dei moderni elaboratori elettronici. Più precisamente, ogni elaboratore dispone di unità dedicate all'ingresso dei dati, analoghe al nastro d'ingresso dell'automa; inoltre, gli ingressi ricevuti modificano lo stato interno del calcolatore. Infine, anche gli elaboratori elettronici organizzano le proprie attività in base ad un ciclo di lavoro.
L'automa a stati finiti deterministico, inoltre, implementa un algoritmo ben preciso, codificato come vedremo nella funzione di transizione.
Sebbene queste analogie siano evidenti, vi sono anche aspetti in cui si riscontrano differenze nette; di questi, due sono particolarmente significativi: la mancanza di dispositivi di uscita e la quasi totale assenza di memoria interna. Gli automi a stati finiti non sono totalmente privi di memoria in quanto devono poter memorizzare il proprio stato.
Va inoltre segnalato che, mentre un calcolatore elettronico è adatto all'esecuzione di qualunque algoritmo, gli automi a stati finiti ne eseguono uno solo: quello per cui sono progettati.
Nella lezione introduttiva al corso abbiamo chiarito che il cardine dell'informatica teorica sono i modelli computazionali, intesi come formalismi pensati per rappresentare la computazione.
Dal momento che i calcolatori sono macchine pensate per eseguire computazioni è inevitabile confrontare le due entità: i moderni computer, in tutte le loro interpretazioni (smartphone, tablet, controllori,...) non sono altro che l'implementazione concreta dei modelli teorici rappresentati dai formalismi.
Come conseguenza, acquisire una buona padronanza dei modelli teorici diventa un requisito indispensabile sia per comprendere al meglio i principi in base ai quali funzionano i dispositivi attualmente disponibili sul mercato, sia e soprattutto per pensarne e progettarne di nuovi.
Struttura della lezione
[modifica]L'obiettivo di questa lezione sarà la presentazione di tre formalismi cui sinteticamente ci si riferisce con il nome di automi:
- gli automi a stati finiti;
- gli automi accettori a stati finiti;
- gli automi trasduttori a stati finiti.
Ogni formalismo verrà presentato seguendo un approccio induttivo, partendo da esempi concreti e cercando di ricavare le proprietà generali dei formalismi stessi. In seguito, le caratteristiche evidenziate in modo intuitivo studiando gli esempi proposti verranno formulate in modo più preciso, ponendo una definizione rigorosa.
La presente lezione è pensata come introduzione ai tre formalismi e si prefigge l'obiettivo di familiarizzare con essi, ponendo l'accento sull'uso degli automi come strumenti utili rappresentare la computazione.
In realtà, proprio perché gli automi sono dei modelli dispongono di proprietà generali di cui, in questo contesto, ci disinteressiamo.
Nella prossima lezione affronteremo l'importante questione delle proprietà degli automi assumendo uno stile molto più formale, basato sull'enunciazione e la dimostrazione di teoremi.
Automa a stati finiti
[modifica]La letteratura classica sugli automi [6] considera il riconoscitore a stati finiti come il punto di partenza per la discussione sugli automi.
In questa lezione si seguirà invece la filosofia del testo di Mandrioli e Ghezzi[7], dove il riconoscitore a stati finiti viene preceduto da un automa più semplice, ideale per introdurre il tema della modellazione.
In realtà gli altri due modelli di automa, ossia gli accettori ed i trasduttori, sono dotati di proprietà molto interessanti e per questo motivo vengono impiegati più frequentemente nel contesto dell'informatica teorica.
Esempio di automa a stati finiti
[modifica]Visto che l'automa a stati finiti può essere impiegato per creare modelli astratti di situazioni concrete, lo sfrutteremo per creare una rappresentazione di una situazione quotidiana: la risposta ad una telefonata.
Descrizione informale della situazione
[modifica]Partiamo anzitutto da una descrizione: un telefono riceve un segnale di chiamata; il proprietario del telefono, a questo punto, può accettare la chiamata oppure rifiutarla. Se decide di accettare la chiamata, conversa per un po' e dopo riattacca.
Analisi della situazione
[modifica]Il protagonista di questo esempio è il telefono, perciò la discussione che segue riguarderà le sue caratteristiche. Leggendo la descrizione precedente si deduce che il telefono può trovarsi in tre condizioni operative: l' attesa, in cui il dispositivo attende una chiamata, la chiamata in cui il dispositivo riceve il segnale di chiamata e la conversazione, in cui viene utilizzato per discutere.
Quando il telefono riceve un segnale l'apparecchio si porta nello stato di chiamata, finché il proprietario deciderà se accettare o meno.
Se il proprietario accetta la chiamata, il telefono si porta nello stato di conversazione, mentre se dovesse rifiutare l'apparecchio tornerebbe nello stato di attesa.
Al termine della conversazione il telefono riceve un segnale di fine chiamata e ritorna nello stato di attesa.
Descrizione dell'automa
[modifica]Per quanto visto finora l'automa dovrà essere in grado di descrivere tre elementi chiave: lo stato in cui si trova il telefono, i segnali che esso deve interpretare ed il modo in cui questi ultimi agiscono sull'evoluzione dello stato. Più formalmente, la descrizione dell'automa avrà bisogno dei seguenti elementi:
- un insieme finito di stati
- un insieme finito di ingressi
- un meccanismo di transizione che permetta di passare da uno stato all'altro quando si ricevono gli ingressi
La descrizione di un automa a stati finiti dovrà comprendere tutti e tre questi elementi; col tempo si sono affermate due tecniche di rappresentazione: la prima di tipo grafico (detta diagramma degli stati), la seconda tipo algebrico; analizzeremo entrambe le alternative.
Il diagramma degli stati
[modifica]Concettualmente il diagramma degli stati è un grafo e come conseguenza conterrà nodi e lati. Si tratta semplicemente di trovare una tecnica grafica per rappresentare questi due concetti.
Nel grafo che rappresenta il diagramma, gli stati dell'automa sono i nodi del grafo e vengono rappresentati attraverso il loro nome, racchiuso in un cerchio. Nell'esempio della telefonata la rappresentazione grafica degli stati è la seguente.

A questo punto mancano solamente i lati del grafo che sono rappresentati tramite frecce, ognuna delle quali contiene un commento che specifica quale simbolo viene letto durante la transizione da uno stato all'altro. In questo modo si completa la descrizione grafica dell'automa; il risultato è visibile nell'immagine sottostante.

Un commento a parte, poi, lo meritano le transizioni; nella lezione introduttiva è stato detto che uno dei modi per rappresentare una transizione consiste nell'impiego di una tripla ordinata di elementi dove indica lo stato attuale, indica l'azione compiuta (e quindi nel nostro caso un simbolo d'ingresso) e indica lo stato prossimo.
Grazie a questa breve descrizione è possibile rappresentare graficamente il concetto di transizione, semplicemente collegando due stati attraverso un arco.
In linea di massima, quindi, un automa potrebbe essere descritto da un elenco di transizioni come quelle visibili nei diagrammi sottostanti.

Come si può notare dal grafico, lo svantaggio di rappresentare le singole transizioni consiste nell'avere una visione frammentata dell'automa, in cui tra l'altro uno stesso stato viene riportato in punti diversi del diagramma. Possiamo immaginare di spostare le singole transizioni muovendole in modo che gli stati con lo stesso nome si sovrappongano perfettamente; il diagramma che si ottiene in questo modo è identico a quello che descrive l'intero automa, a dimostrazione del fatto che il diagramma degli stati di un automa è un modo sintetico per rappresentare l'elenco di tutte le possibili transizioni. L'immagine sottostante illustra questo aspetto mediante un'animazione.

Descrizione algebrica
[modifica]La descrizione algebrica di un automa a stati finiti consiste nell'elencazione delle caratteristiche dell'automa impiegando insiemi e funzioni. Vediamo questa tecnica all'opera nel caso della chiamata telefonica.
Indicando con la lettera l'insieme degli stati avremo:
Indicando con la lettera l'insieme dei simboli di ingresso avremo:
Restano da definire le transizioni. Nella lezione introduttiva abbiamo delineato due possibili tecniche per la rappresentazione delle transizioni ed una delle due consisteva nel pensare la transizione come una funzione che associa al massimo uno stato prossimo alle coppie costituite da uno stato attuale e da un ingresso. Tale funzione prende il nome di funzione di transizione; considerando che disponiamo di un numero finito di stati e di un numero finito di simboli d'ingresso, avremo anche un numero finito di coppie (stato, ingresso). In questa situazione, una possibilità per rappresentare la funzione di transizione consiste nell'impiego di una tabella; nell'esempio visibile di seguito le righe della tabella rappresentano gli stati, le colonne rappresentano gli ingressi ed ogni singolo elemento rappresenta lo stato prossimo.
| ricezione | accettazione | rifiuto | conclusione | |
|---|---|---|---|---|
| Attesa | Chiamata | - | - | - |
| Chiamata | - | Conversazione | Attesa | - |
| Conversazione | - | - | - | Attesa |
Un aspetto importante nella definizione della funzione riguarda il fatto che essa non è necessariamente definita per tutte le possibili coppie , come testimonia la tabella soprastante; la funzione è, in generale, una funzione parziale.
Completezza degli automi
[modifica]Il fatto che la funzione di transizione di un automa a stati finiti possa non essere definita per ogni simbolo di ingresso può rappresentare un problema; infatti, quando studieremo le proprietà formali degli automi a stati finiti scopriremo che molte di esse valgono solamente se la funzione di transizione è sempre definita.
Vista l'importanza dell'argomento, gli automi a stati finiti vengono in generale suddivisi in due categorie: quelli completi, in cui la funzione di transizione è definita in ogni punto del suo insieme di partenza e quelli incompleti, nei quali la funzione di transizione è parziale.
Per lo studio delle proprietà degli automi impiegheremo sempre automi completi; questo ci pone di fronte ad un interessante problema: cosa fare se l'automa che ci interessa è incompleto? La risposta a questa domanda è duplice: da un lato si sta cercando di generalizzare le proprietà dimostrando che valgono anche quando gli automi sono incompleti, dall'altro si è definita una procedura che consente di alterare la struttura dell'automa incompleto, facendo in modo che la sua funzione di transizione diventi totale e quindi ovunque definita.
Il completamento di un automa
[modifica]La tecnica impiegata per completare un automa è molto semplice e consiste nell'aggiunta di uno stato (che potrebbe avere il significato di stato d'errore ed è spesso chiamato sink state nella letteratura inglese) e di una revisione delle transizioni, in modo da garantire i due requisiti seguenti:
- da ognuno degli stati originari deve partire un numero di transizioni esattamente uguale alla cardinalità dell'alfabeto d'ingresso;
- una volta raggiunto lo stato di errore non deve essere più possibile abbandonarlo.
L'automa a stati finiti presentato come esempio è un automa incompleto: ce ne possiamo accorgere ispezionando il suo diagramma degli stati e notando, ad esempio, che dallo stato di attesa parte una sola transizione sulle quattro possibili. È quindi possibile realizzare una versione completa dell'automa, il cui diagramma degli stati è riportato di seguito.

Oltre al diagramma degli stati è necessario esaminare cosa accade, nel caso del completamento, anche a livello algebrico; proprio per questo motivo, riportiamo di seguito la descrizione algebrica della versione completa dell'automa.
- ;
- ;
- la funzione di transizione, , è riportata qui sotto.
| ricezione | accettazione | rifiuto | conclusione | |
|---|---|---|---|---|
| Attesa | Chiamata | Errore | Errore | Errore |
| Chiamata | Errore | Conversazione | Attesa | Errore |
| Conversazione | Errore | Errore | Errore | Attesa |
| Errore | Errore | Errore | Errore | Errore |
Da un punto di vista algebrico, quindi, la modifica apportata consiste nell'aggiunta di una riga (corrispondente all'aggiunta di uno stato) e dalla sostituzione di tutti gli elementi non definiti con riferimenti allo stato di errore.
In questo modo lo stato di errore diventa lo stato prossimo di tutte le transizioni che in precedenza non erano state definite; inoltre, una volta raggiunto tale stato, se anche l'automa ricevesse altri simboli d'ingresso non sarebbe in grado di abbandonarlo.
Definizione di automa a stati finiti deterministico
[modifica]Un automa a stati finiti deterministico è una tripla ordinata di elementi (Q, I, ) così definiti:
- Q è un insieme finito di stati;
- I è un insieme finito di simboli e si chiama alfabeto d'ingresso;
- è una funzione che associa ad ogni coppia ordinata formata dallo stato attuale dell'automa e dall'ingresso attuale, al massimo uno stato detto stato prossimo.
Funzione di transizione generalizzata
[modifica]La funzione di transizione che compare nella definizione di automa a stati finiti accetta come argomento un simbolo scelto dall'alfabeto di partenza.
Normalmente, tuttavia, l'automa opera su stringhe di simboli; è quindi possibile definire una funzione di transizione generalizzata, che accetta come argomenti lo stato attuale ed una stringa di simboli di ingresso provenienti dal monoide libero generato dall'alfabeto di ingresso e dalla funzione di concatenazione: . La funzione è definita per ricorrenza come segue:
La notazione impiegata per indicare la funzione di transizione generalizzata, ossia l'operatore star di Kleene, indica che si tratta di una chiusura riflessiva e transitiva della funzione di transizione.
Automa accettore
[modifica]L'automa accettore a stati finiti deterministico rappresenta un primo tentativo di superare le limitazioni associate all'automa a stati finiti analizzato nella lezione precedente.
Più precisamente, l'automa accettore introduce un rudimentale meccanismo di uscita, che permette di avere informazioni più complete circa lo stato dell'automa. Anche in questo caso è possibile immaginare l'automa come un elaboratore piuttosto rudimentale, riportato nella figura sottostante.
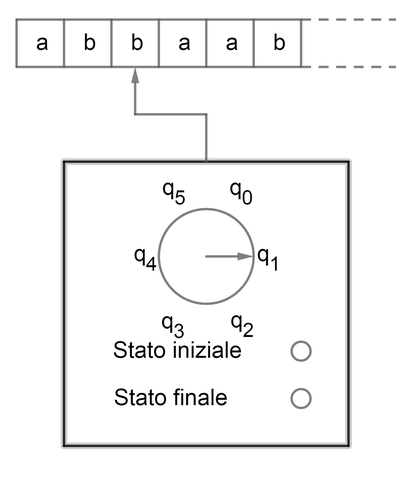
Oltre al nastro di ingresso ed agli stati, l'immagine mostra anche due indicatori: uno per lo stato iniziale, l'altro per lo stato finale. È possibile associare un significato all'indicatore per lo stato finale: possiamo immaginarlo come una luce che si accende in corrispondenza di particolari sequenze di ingresso e rimane spenta leggendone altre. Questo comportamento può essere interpretato come una risposta del tipo "si o no" oppure "vero o falso" ad una domanda che, in qualche modo, è codificata sul nastro d'ingresso. Tutte le sequenze di simboli d'ingresso che provocheranno l'accensione dell'indicatore di stato finale corrisponderanno ad una risposta positiva e si dirà che saranno accettate dall'automa; questo spiega, tra l'altro, la particolare denominazione scelta per il presente formalismo.
Principio di funzionamento dell'automa
[modifica]Anche l'automa accettore a stati finiti dispone di un ciclo di lavoro, del tutto analogo a quello dell'automa descritto nella lezione precedente; si tratta quindi di un procedimento in due fasi: la prima è dedicata alla lettura di un simbolo dal nastro d'ingresso e la seconda è data dall'aggiornamento dello stato. L'unica differenza consiste nel fatto che, durante l'aggiornamento, viene evidenziato il passaggio attraverso degli stati finali.
Un esempio dalla bioinformatica.
[modifica]Uno dei processi biologici che hanno luogo all'interno della cellula è la produzione delle proteine, attività che si articola in due fasi principali: la trascrizione e la traduzione. La trascrizione consiste nella produzione di un singolo filamento di RNA messaggero a partire dal DNA. La traduzione ha sede in strutture cellulari chiamate ribosomi, dove il filamento di RNA messaggero viene trasformato in una catena di amminoacidi.
Il problema che vogliamo affrontare riguarda la trascrizione e più precisamente il funzionamento dell'enzima della RNA polimerasi, principale responsabile della produzione del filamento di RNA messaggero. Affinché l'enzima possa agire deve anzitutto legarsi al DNA nel punto giusto e proprio per questo motivo il DNA dispone di sequenze di nucleotidi opportunamente strutturate, dette promotori della polimerasi. Nel caso delle cellule appartenenti ad organismi eucarioti il promotore è costituito dalla sequenza di sei nucleotidi T, A, T, A, A, A.
A questo punto disponiamo di tutti gli elementi per formalizzare il problema. Consideriamo un alfabeto composto da quattro simboli: che rappresentano i nucleotidi del DNA; le stringhe di simboli costruite a partire da questo alfabeto rappresentano quindi filamenti di DNA. Il nostro obiettivo è realizzare un automa a stati finiti che identifichi la prima istanza del promotore della RNA polimerasi all'interno di una stringa di DNA.
Procediamo anzitutto con la descrizione completa dell'automa, identificandone gli elementi caratteristici.
Insieme degli stati
[modifica]L'automa possiede sette stati:
- : non è stato identificato nessun nucleotide appartenente al promotore
- : è stata identificata la prima timina
- : è stata identificata la sequenza T, A
- : è stata identificata la sequenza T, A, T
- : è stata identificata la sequenza T, A, T, A
- : è stata identificata la sequenza T, A, T, A, A
- : è stata identificata la sequenza T, A, T, A, A, A
Possiamo anche aggiungere che lo stato è lo stato iniziale e che lo stato ha un significato particolare, in quanto indica il riconoscimento del promotore; tale stato viene detto finale o anche di accettazione.
Alfabeto d'ingresso
[modifica]Come abbiamo anticipato nella descrizione informale del problema, l'alfabeto d'ingresso contiene i simboli A, C, G, T che rappresentano i nucleotidi del DNA.
Funzione di transizione
[modifica]La funzione di transizione verrà fornita sfruttando la rappresentazione tabellare, possibile quando gli insiemi di partenza e di arrivo contengono un numero finito di elementi.
In questo caso una descrizione verbale della funzione di transizione è piuttosto semplice: se la sequenza di simboli letti dall'automa combacia con uno qualsiasi dei prefissi della stringa che indica il promotore, l'automa dovrebbe evolvere passando allo stato successivo, in caso contrario dovrebbe invece tornare allo stato . Questo comportamento generale ammette due eccezioni: una nello stato dove, se viene letto un simbolo si effettua una transizione allo stato anziché a ; in modo analogo, se nello stato viene letto un simbolo , lo stato rimane anziché diventare . Grazie a questa osservazione possiamo compilare la seguente tabella:
| A | T | G | C | |
|---|---|---|---|---|
| - | - | - | - |
Si noti come due degli stati siano evidenziati rispetto agli altri: uno è lo stato iniziale, indicato da una freccia, l'altro è lo stato di accettazione, indicato da un asterisco. Questa notazione è stata introdotta nel 1969 da Hopcroft ed Ullman e ha trovato da allora ampia accettazione fra gli addetti ai lavori.
Diagramma degli stati
[modifica]In alternativa alla rappresentazione dell'automa a stati basata sugli insiemi é possibile fornire una rappresentazione grafica, più sintetica e facilmente leggibile, dalla quale si possono dedurre tutti gli elementi dell'automa.

Per brevità, più simboli sono stati associati alle transizioni.
In questa rappresentazione riconosciamo due novità: la freccia davanti a serve per indicare lo stato iniziale, mentre il bordo raddoppiato attorno a indica uno stato di accettazione.
Grazie alla descrizione che abbiamo svolto è possibile caratterizzare l'automa . Tale descrizione, tuttavia, omette due informazioni: non vengono specificati né lo stato iniziale né quello finale. La descrizione che si ottiene aggiungendo questi due elementi porta in modo naturale alla definizione di automa accettore a stati finiti.
Osservazioni
[modifica]Osservando la tabella che definisce la funzione di transizione si nota che per ogni possibile coppia ordinata costituita da uno stato e da un simbolo d'ingresso esiste uno ed un solo stato prossimo. Le funzioni che verificano questa condizione prendono il nome di funzioni totali e si contrappongono alle funzioni parziali di cui parleremo in seguito.
L'osservazione della tabella permette anche di notare come le ultime due colonne, riguardanti i simboli d'ingresso e , siano sempre associate allo stato prossimo . Questo particolare dipende dal fatto che la sequenza da riconoscere non contiene nessuno dei due simboli; d'altra parte includere e nell'alfabeto è indispensabile in quanto sono presenti nelle stringhe di DNA.
Un'ultima osservazione riguarda invece il modo in cui abbiamo affrontato il problema: la situazione iniziale, formulata nel dominio della biologia, è stata trasformata in un problema di ricerca di testo in una stringa, descritto poi dall'automa proposto. Questa seconda versione del problema è evidentemente semplificata rispetto a quella originale in quanto, ad esempio, non si considera il modo in cui i nucleotidi sono legati tra loro a formare la stringa di DNA.
La versione semplificata del problema prende il nome di modello ed il processo che consente di passare dal problema al modello si chiama modellazione. La modellazione implica sempre la scelta di un formalismo adatto a rappresentare la versione semplificata del problema; in tal senso gli automi a stati finiti possono essere pensati come formalismi adatti a costruire modelli, supportando i progettisti nella delicata fase di traduzione che caratterizza la fase iniziale della soluzione di ogni problema.
Definizione di automa accettore
[modifica]Un automa accettore a stati finiti, detto anche riconoscitore a stati finiti, è una quintupla ordinata di elementi definiti come segue:
- è un insieme finito di stati;
- è un insieme finito di simboli d'ingresso;
- è la funzione di transizione;
- prende il nome di stato iniziale;
- prende il nome di insieme degli stati di accettazione o anche di insieme degli stati finali.
Gli elementi , considerati separatamente, costituiscono l'automa soggiacente all'accettore. Questa considerazione evidenzia il fatto che l'automa accettore è un'estensione dell'automa a stati finiti, cui aggiunge i concetti di stato iniziale e di insieme degli stati di accettazione.
I singoli elementi dell'insieme prendono il nome di stati di accettazione o indifferentemente stati finali.
Il concetto di accettazione
[modifica]Quando un automa accettore riceve una stringa in ingresso l'elaborazione può terminare in due modi, a seconda che l'ultimo stato appartenga all'insieme degli stati finali oppure no.
Quando l'elaborazione termina in uno degli stati finali, si dice che la stringa in ingresso è accettata dall'automa. Da un punto di vista più rigoroso, diremo che una stringa è accettata dall'automa accettore a stati finiti se e solo se .
L'insieme di tutte le stringhe accettate dall'automa costituisce un sottoinsieme del monoide libero costruito sull'alfabeto di ingresso e quindi, per definizione, costituisce un linguaggio. Il linguaggio accettato dall'automa è dunque l'insieme di tutte le stringhe accettate e prende il nome di linguaggio macchina.
Più precisamente, indicando con il linguaggio macchina dell'automa , possiamo scrivere: .
Conseguenze dell'accettazione
[modifica]Sappiamo che ogni automa accettore è dotato di un proprio linguaggio, composto dalle stringhe che l'automa stesso è in grado di accettare.
In generale accettori diversi corrisponderanno a linguaggi differenti e viene spontaneo chiedersi quali caratteristiche permettano ad un riconoscitore a stati finiti di determinare il proprio linguaggio macchina. La risposta a questo interrogativo è tutta nella funzione di transizione in quanto è la sequenza delle transizioni a determinare l'accettazione o meno di una stringa.
Dato che la funzione di transizione rappresenta l'algoritmo realizzato dall'accettore, si conclude che il linguaggio macchina dell'automa accettore è determinato dall'algoritmo implementato dall'automa stesso.
È quindi pensabile stabilire una corrispondenza tra gli automi ed i linguaggi definiti sul monoide libero generato dall'alfabeto di ingresso. La relazione esistente tra queste entità merita un'analisi più approfondita: sarà vero che per ogni possibile accettore esiste un linguaggio associato? Sarà vero che per ogni possibile linguaggio esiste un automa riconoscitore associato? La risposta a questi interrogativi verrà data nella prossima lezione, studiando le proprietà formali degli accettori a stati finiti.
Computazione negli automi a stati finiti
[modifica]Gli automi a stati finiti sono formalismi concepiti per rappresentare la computazione. Finora abbiamo esaminato due tecniche per rappresentare gli automi ma non abbiamo ancora visto come questi ultimi possano sviluppare una computazione.
Per raggiungere questo obiettivo dovremo anzitutto introdurre il concetto di configurazione e discutere successivamente come, attraverso sequenze di configurazioni, sia possibile parlare di transizioni e più in generale di computazione.
La configurazione di un accettore a stati finiti
[modifica]La configurazione di un accettore a stati finiti è una coppia ordinata , dove il primo elemento è uno stato dell'automa ed il secondo elemento è la parte della stringa di ingresso che dev'essere ancora letta.
La computazione operata dagli automi a stati finiti è quindi una successione di configurazioni; richiamando quanto detto nella lezione introduttiva, si vede che la configurazione è un modo per rappresentare il passo della computazione e che la strategia scelta per scrivere i passi è quella di riportare la coppia stato-azione.
Negli accettori a stati finiti esistono due tipi di configurazione che meritano attenzione particolare:
- configurazione iniziale: rappresentata dalla coppia , dove indica lo stato iniziale dell'accettore e indica l'intera stringa da riconoscere;
- configurazione finale: rappresentata dalla coppia , dove è uno stato finale e la presenza della stringa vuota indica che tutta la stringa di ingresso è già stata letta dall'automa.
Rappresentazione della computazione
[modifica]Una transizione può essere pensata come il passaggio tra due configurazioni consecutive; siano quindi e due configurazioni consecutive. Allora la transizione che porta da a si indicherà con .
Grazie a questa notazione diventa possibile rappresentare l'intera computazione svolta dall'accettore semplicemente riportando la sequenza delle transizioni effettuate.
In particolare, la computazione di una stringa appartenente al linguaggio macchina dell'automa consiste in una successione finita di configurazioni nella quale la prima è una configurazione iniziale e l'ultima è una configurazione finale.
Chiariamo il concetto con un esempio pratico, considerando un automa che sia in grado di riconoscere un numero naturale dispari codificato in binario.
La scelta della codifica binaria ci porta a concludere che l'alfabeto dell'automa sarà .
Quando un numero naturale viene codificato in binario, tutti i numeri dispari terminano con la cifra 1. Un automa a stati finiti in grado di riconoscere numeri di questo tipo dovrà accettare tutte le stringhe composte dai simboli zero e uno che terminano con un uno.
Per raggiungere questo obiettivo si può predisporre l'automa visibile nell'immagine sottostante.

La descrizione algebrica dell'automa prevede i seguenti elementi:
- ;
- ;
- ;
- ;
La funzione di transizione è riportata di seguito.
| 0 | 1 | |
|---|---|---|
Basandoci sull'accettore a stati finiti appena costruito rappresentiamo la computazione riguardante la stringa 10110111, che codifica in binario il numero naturale dispari 183.
La computazione attraversa nove configurazioni; inoltre la prima è la configurazione iniziale e l'ultima è una configurazione finale, a dimostrazione del fatto che la stringa è accettata dall'automa.
Impiegando lo stesso accettore rappresentiamo la computazione riguardante il numero 10110, che codifica in binario il numero naturale pari 22.
In questo caso sono bastate sei configurazioni; la prima è la configurazione iniziale mentre l'ultima non è una configurazione finale, pertanto la stringa non è stata accettata dall'automa.
Accettazione di stringhe
[modifica]Il simbolo di transizione che abbiamo appena introdotto è utile per rappresentare sinteticamente il passaggio da una configurazione ad un'altra in corrispondenza alla lettura di un solo simbolo dal nastro d'ingresso.
Può capitare di dover rappresentare il cambiamento delle configurazioni in corrispondenza alla lettura di una stringa dal nastro d'ingresso.
Si consideri a tal proposito un accettore a stati finiti e tre stringhe tali che . Si considerino poi due stati e e due configurazioni e . Come si può notare, la seconda configurazione è stata ottenuta leggendo dal nastro d'ingresso tutti i simboli della stringa e da questo punto di vista si può dire che è un suffisso di .
Per rappresentare sinteticamente l'insieme delle transizioni che l'automa ha effettuato per passare dalla prima alla seconda configurazione si può scrivere , dove l'asterisco indica il consueto operatore star di Kleene.
Una delle situazioni in cui questa notazione ha più senso si trova nell'accettazione di una stringa; ad esempio, considerando il riconoscitore di numeri dispari codificati in binario, il riconoscimento della stringa 10110111 si potrà scrivere . Questa notazione mette ben in evidenza il fatto che la prima è una configurazione iniziale (a causa della presenza dello stato ) e che la seconda è una configurazione finale ( e l'automa ha letto l'intera stringa).
Automa trasduttore
[modifica]Finora abbiamo analizzato due formalismi: gli automi a stati finiti e gli accettori. Il secondo tipo è stato introdotto per cercare di superare un'importante limitazione associata agli automi a stati finiti, ossia la mancanza di un dispositivo di uscita; la soluzione proposta dagli accettori è molto rudimentale e consente di determinare solamente lo stato iniziale e gli stati finali.
Gli automi trasduttori risolvono definitivamente il problema, disponendo di un nastro di uscita su cui vengono riportati dei simboli.
Come vedremo, questa modifica influenzerà in maniera importante la rappresentazione algebrica dell'automa, rendendola più pesante; d'altra parte, la possibilità di ottenere un feedback costituito da simboli aumenta in modo significativo l'utilità di questi formalismi, specialmente per quanto concerne le problematiche riguardanti la modellazione. Infatti, grazie all'introduzione del nastro d'uscita l'automa ha la possibilità di reagire in due modi alla ricezione di un simbolo d'ingresso: la consueta transizione di stato e la produzione di un simbolo o di una stringa di simboli.
Principio di funzionamento dell'automa trasduttore
[modifica]Come è già successo per gli automi a stati finiti e per gli accettori, è possibile immaginare il trasduttore a stati finiti come una macchina, la cui struttura è rappresentata schematicamente nell'immagine sottostante.

La macchina funziona seguendo un ciclo di lavoro composto da tre passi:
- lettura di un simbolo in ingresso
- evoluzione dello stato
- produzione di simboli in uscita
La vera novità è costituita dal terzo passo, dove un dispositivo di scrittura riporta su un nastro d'uscita un simbolo, o una stringa di simboli derivati da un alfabeto che, in generale, è diverso da quello di ingresso.
L'informazione da riprodurre sul nastro d'uscita viene decisa in base allo stato attuale dell'automa ed al particolare simbolo di ingresso che è stato letto.
Come di consueto l'automa trasduttore verrà introdotto a partire da un esempio pratico; la discussione che ne scaturirà servirà per identificare le caratteristiche chiave del modello che troveranno poi una sintesi nella definizione posta a fine lezione.
Un esempio dal settore dell'automazione
[modifica]Uno degli aspetti che riguardano la gestione di un autosilo concerne l'ammissione dei veicoli. Affinché un veicolo abbia diritto ad accedere all'autosilo il conducente deve prima munirsi di un biglietto che verrà utilizzato sia per contabilizzare la spesa sia per consentire l'uscita dal parcheggio.
Fisicamente, l'accesso all'autosilo è gestito da un sistema composto da tre unità:
- l'unità esterna si occupa di emettere il biglietto che consente l'accesso al parcheggio;
- l'asta impedisce o consente il passaggio del veicolo;
- l'unità interna si assicura che il veicolo sia entrato completamente nell'autosilo prima di abbassare la sbarra.
La procedura di ammissione si articola nei seguenti quattro punti:
- il guidatore, giunto all'ingresso dell'autosilo, preme un pulsante per richiedere l'accesso;
- a seguito della pressione del pulsante l'unità esterna emette un biglietto e rimane in attesa che il conducente lo prelevi;
- quando il guidatore preleva il biglietto l'asta si alza consentendo il passaggio del veicolo;
- il passaggio del veicolo viene rilevato da un sensore e, quando il veicolo ha attraversato lo sbarramento d'ingresso, l'asta si abbassa; a questo punto il sistema si mette in attesa del prossimo cliente.
Questa breve descrizione permette di comprendere come il sistema che ci apprestiamo a studiare possa interagire con il mondo circostante in due modi:
- ricevendo stimoli dall'esterno, ad esempio con la pressione del pulsante o con il ritiro del biglietto;
- fornendo stimoli all'esterno, ad esempio con l'emissione del biglietto o con l'azionamento dell'asta.
Fino a questo punto gli stimoli provenienti dall'esterno sono stati rappresentati da simboli appartenenti ad un alfabeto d'ingresso; per analogia, gli stimoli forniti all'esterno saranno quindi rappresentati da simboli appartenenti ad un alfabeto d'uscita, una naturale estensione del formalismo. Esaminiamo ora gli elementi caratteristici dell'automa.
Insieme degli stati
[modifica]L'automa è caratterizzato da tre stati:
- : in questo stato si attende l'arrivo di un veicolo;
- : in questo stato si elabora la richiesta di accesso all'autosilo;
- : in questo stato si conclude l'ammissione del veicolo.
In aggiunta a queste informazioni, diremo che è lo stato iniziale e che non c'è alcuno stato finale.
Alfabeto d'ingresso
[modifica]L'alfabeto di ingresso è costituito da tre simboli:
- : indica la richiesta di accesso all'autosilo;
- : indica che il biglietto è stato prelevato;
- : indica che il veicolo è entrato nell'autosilo.
Funzione di transizione
[modifica]Basandoci sulle informazioni appena identificate è possibile sviluppare la funzione di transizione sottostante:
| - | - | ||
| - | - | ||
| - | - |
Si può notare che gran la funzione di transizione è parziale, in quanto non associa uno stato prossimo a tutte le possibili coppie di stati e simboli d'ingresso. In situazioni come questa c'è la possibilità di descrivere la funzione di transizione utilizzando una forma diversa da quella proposta: il grafo.
Concettualmente, il grafo è un elenco di tutte le coppie che caratterizzano la funzione; comprensibilmente, il grafo è uno strumento interessante quando il numero di coppie è finito.
Per adattare la definizione di grafo alla nostra situazione bisogna considerare che gli argomenti della funzione sono costituiti da coppie ordinate, quindi ogni elemento del grafo sarà dato da tre entità: una coppia ed un singolo valore riguardante lo stato prossimo. Una rappresentazione insiemistica del grafo della funzione sarà: . È possibile riportare gli elementi del grafo in una tabella, visibile di seguito.
| Stato attuale | Simbolo d'ingresso | Stato prossimo |
| r | ||
| p | ||
| a |
Definizione dell'accettore
[modifica]Sulla base degli elementi identificati in precedenza è possibile immaginare un automa accettare a stati finiti in cui i cinque elementi sono caratterizzati come segue:
- ;
- ;
- è dotata del seguente grafo ;
- è lo stato iniziale;
- in quanto non ci sono stati finali.
Estensione dell'automa accettore
[modifica]La descrizione offerta fino a questo punto non è completa in quanto non considera l'interazione del sistema con l'ambiente circostante. È qui che entrano in gioco tre aspetti: l'emissione del ticket, l'innalzamento e l'abbassamento della sbarra. Ad ognuna di queste azioni è possibile associare un simbolo:
- indica l'emissione del biglietto;
- indica il sollevamento della sbarra;
- indica l'abbassamento della sbarra.
Questi simboli si possono raccogliere in un insieme finito che rappresenta l'alfabeto d'uscita.
Definire questo insieme non è tuttavia sufficiente: è necessario chiarire in base a quali meccanismi vengano emessi i simboli dell'alfabeto appena creato. La logica che sta dietro all'emissione dei simboli è la stessa che guida la funzione di transizione. Potremo quindi immaginare una funzione , detta funzione d'uscita, che associ ad ogni coppia ordinata composta da uno stato e da un simbolo d'ingresso al massimo una stringa composta da simboli dell'alfabeto d'uscita. Forniamo di seguito la rappresentazione tabellare di tale funzione.
| - | - | ||
| - | - | ||
| - | - |
Analogamente a quanto visto per la funzione di transizione è possibile offrire una descrizione basata sul grafo sottostante.
| Stato attuale | Simbolo d'ingresso | Stringa di uscita |
| T | ||
| U | ||
| D |
La definizione dell'alfabeto di uscita e della funzione d'uscita ci permetterebbero di estendere la definizione di automa accettare arrivando; tuttavia, prima di parlare degli automi trasduttori, esaminiamo il diagramma degli stati associato a questo tipo di automa.
Diagramma degli stati
[modifica]Nell'immagine sottostante è riportato il diagramma degli stati per l'automa che rappresenta un modello per la gestione dell'autosilo.

Come si può notare, gli archi che rappresentano le transizioni contengono più informazioni: ognuno di essi, infatti, è etichettato con una coppia di simboli , dove e .
Definizione di automa trasduttore
[modifica]L'automa trasduttore è una 7-upla ordinata di elementi definiti come segue:
- è un insieme finito di stati;
- è un insieme finito di simboli d'ingresso;
- è la funzione di transizione;
- è lo stato iniziale;
- è l'insieme degli stati di accettazione;
- è un insieme finito di simboli detto alfabeto d'uscita;
- è la funzione d'uscita.
In particolare, la funzione associa ad ogni coppia ordinata costituita da uno stato e da un simbolo d'ingresso al massimo una stringa ottenuta a partire dall'alfabeto d'uscita.
Gli elementi , presi separatamente, costituiscono l'accettore soggiacente al trasduttore . Questo dimostra che l'automa trasduttore a stati finiti è un'estensione dell'accettore a stati finiti che abbiamo già analizzato in precedenza.
La funzione di uscita generalizzata
[modifica]Leggendo la definizione del trasduttore si nota che la funzione di uscita può produrre anche più di un simbolo in corrispondenza di una sola transizione. Ha senso chiedersi cosa accada quando, anziché avere in ingresso un solo simbolo, vi sarà un'intera stringa.
La situazione che desideriamo analizzare è simile a quella incontrata studiando le transizioni negli automi a stati finiti e che aveva portato alla definizione della funzione di transizione generalizzata.
In modo analogo è possibile introdurre la funzione di uscita generalizzata, indicata con il simbolo e definita per induzione come segue:
Dove e con il simbolo si indica la concatenazione tra stringhe.
La traduzione
[modifica]L'automa trasduttore associa ad ogni stringa ricavata dall'alfabeto di ingresso una corrispondente stringa ricavata dall'alfabeto di uscita.
Come accadeva per gli automi accettori, anche gli automi trasduttori sono dotati di un linguaggio macchina, inteso come l'insieme delle stringhe dell'alfabeto di ingresso che vengono accettate dall'automa.
Negli automi trasduttori ogni stringa appartenente al linguaggio macchina viene tradotta in una stringa ricavata dall'alfabeto di uscita.
Si può pensare di raccogliere in un insieme tutte le stringhe di uscita generate a partire da stringhe del linguaggio macchina; questo insieme è naturalmente un sottoinsieme del monoide libero generato sull'alfabeto di uscita e quindi è anch'esso un linguaggio.
Si può concludere che l'automa trasduttore è in grado di trasformare le stringhe del linguaggio macchina in stringhe appartenenti ad un altro linguaggio; questa operazione prende il nome di traduzione e può essere formalmente definita come segue:
In questa definizione il simbolo indica la funzione di traduzione e la lettera indica una generica stringa ricavata dall'alfabeto di ingresso. Come si vede, la definizione pone come condizione aggiuntiva l'accettazione della stringa, in modo da avere la garanzia che solamente le stringhe appartenenti al linguaggio macchina vengano tradotte.
Una curiosità: la programmazione basata su automi
[modifica]Prima di concludere la lezione è interessante riportare un'applicazione molto concreta dell'argomento fin qui trattao, ossia la programmazione basata su automi (automata based programming).
Si tratta di un paradigma di programmazione in cui il software viene sviluppato basandosi sulla logica di funzionamento delle macchine a stati; nei programmi sviluppati seguendo questa filosofia sono facilmente riconoscibili tutti gli elementi che abbiamo incontrato in questa lezione introduttiva agli automi e più precisamente gli stati, gli ingressi, le transizioni e le uscite.
L'adozione di questa tecnica ammette, in generale, l'innegabile vantaggio di ridurre il numero di istruzioni di iterazione e / o di selezione necessarie per lo svolgimento di un compito; grazie a questo accorgimento il software ottiene un sensibile miglioramento delle prestazioni.
Al di là della semplice curiosità, la programmazione basata su automi trova impiego in settori molto delicati come quello dei compilatori e degli interpreti, quello della gestione della concorrenza e quello dell'elaborazione dei segnali digitali (con notevoli applicazioni negli ambiti audio e video).
Un altro settore in cui si riscontra un impiego massiccio di questo modello di programmazione è quello dello sviluppo dei videogiochi, dove il modello dell'automa a stati finiti viene impiegato sia per gestire i passaggi di livello nei giochi di tipo arcade, sia per gestire le interazioni tra i personaggi nei più evoluti giochi di ruolo.
Va segnalato inoltre l'interessamento, sia ai formalismi sia a questo paradigma di programmazione, da parte della bioinformatica dove negli ultimi vent'anni gli sviluppi sullo studio della genetica e della biologia molecolare in genere hanno richiesto (e richiederanno) la realizzazione di software pensati per l'analisi di massicce quantità di dati.
Conclusioni
[modifica]La presente lezione è servita per introdurre tre formalismi chiave per la comprensione di alcuni aspetti riguardanti la computazione: gli automi a stati finiti, gli accettori a stati finiti ed i trasduttori a stati finiti.
I tre modelli computazionali sono stati presentati e discussi da un punto di vista fortemente descrittivo e superficiale, senza lasciare spazio a speculazioni riguardanti le loro proprietà. Si è ritenuto di procedere in questo modo per offrire agli studenti la possibilità di entrare in contatto con tali modelli senza incontrare subito le difficoltà riguardanti lo studio e l'analisi delle loro pur importanti proprietà formali.
Una volta acquisita una sufficiente padronanza con il linguaggio e con la progettazione degli automi a stati finiti sarà necessario offrire una visione più dettagliata del loro potenziale, inserendoli nel più ampio contesto dell'informatica teorica.
Appuntamento alla prossima lezione.
Note
[modifica]Bibliografia
[modifica]- Dino Mandrioli e Carlo Ghezzi, Informatica teorica, Milano, CittàStudi, 1999, ISBN 978-8825172416.
- Jeffrey D. Ullman, John Hopcroft e Rajeev Motwani, Introduction to Automata Theory, Languages and Computation, Addison-Wesley, 2006, ISBN 978-0321455369.
- Warren McCulloch, Walter Pitts, A logical calculus of the ideas immanent to neural activity (PDF), in Bullettin of Mathematical Biophysics, vol. 5, 1943.
- David A. Huffman, The synthesis of sequential switching circuits (PDF), in Journal of the Franklin Institute, 1954.
- George H. Mealy, A method for synthesizing sequential circuits, in Bell System Technical Journal, 1955.
- Edward F. Moore, Gedanken experiments on sequential machines, in Automata Studies, Princeton, New Jersey, Princeton University Press, 1956.
| Lezione precedente: Introduzione allo studio dell'informatica teorica | Corso: Materia:Informatica Teorica | Prossima lezione: Teoremi sugli automi a stati finiti |































































































