Funzioni Void e non Void (superiori)
Funzioni
[modifica]Come è stato detto precedentemente le funzioni vengono usate per risolvere problemi parametrici, il fatto di concentrare le istruzioni per risolvere un particolare problema in una sezione limitata del codice (quella fra le { } ) permette di trovare eventuali errori più semplicemente , il fatto di scrivere il codice della funzione solo una volta e di poterlo richiamare successivamente facendo corrispondere i parametri attuali (quelli della chiamata) con quelli della dichiarazione (formali) consente una maggior compattezza del codice e in presenza di eventuali modifica della funzione ( ad esempio se l'iva del calcolo passa dal 20% al 21%) di dover mettere mano solo all'interno del codice della funzione e di aver automaticamente aggiornato il funzionamento in tutto il resto del programma ( nei diversi punti di chiamata). Inoltre l'uso delle funzioni permette l'utilizzo di conoscenze di altri programmatori semplicemente tramite una chiamata alla funzione. Ora vediamo di evedenziare altre caratteristiche.
Funzioni Void e Funzioni non void
[modifica]Le funzioni del C si dividono in funzioni void e non void (quelle dove possiamo restituire un valore tramite l'istruzione return). Ora noi le abbiamo distinte dicendo se si restituisce un solo singolo valore usiamo quelle non void altrimenti usiamo quelle void, in realta' più che sul numero di parametri restituiti dobbiamo porre la nostra attenzione sulla modalità di restituzione del risultato, quando abbiamo una funzione non void, il valore restituito tramite return permette di inserire il risultato in una espressione di calcolo, mentre le funzioni void non possono farlo e si limitano al massimo a restituire uno o più valori (usando dei puntatori) in specifiche celle di memoria il cui indirizzo è passato in fase di chiamata della funzione usando i parametri attuali. Quindi se vogliamo scrivere una funzione che può essere inserita in una espressione di calcolo (cioè che si combina con il calcolo di una espressione matematica) usiamo le funzioni non void altrimenti usiamo le funzioni void. Pensiamo al calcolo di (-b-sqrt(delta) )/(2*a) sqrt è una funzione non void che calcola sqrt(delta) e il risultato di questo calcolo viene inserito nella più ampia espressione (-b -sqrt(delta)).... al posto della chiamata sqrt(delta)
Pensiamo di scrivere una funzione che calcoli il doppio di un numero
float doppio(float n)
{ float z;
z=2*n;
return z;
}
che poteva essere anche scritta come
float doppio(float n)
{
return 2*n;
}
perché quello che viene restituito è il valore dell'espressione (una volta calcolato) dopo l'istruzione return, ricordate inoltre che la funzione termina dopo aver restituito il valore e quindi eventuali istruzioni dopo il return non vengono eseguite, la funzione termina anche se incontra la } di chiusura del codice della funzione.
Ora, una volta scritta la funzione doppio, possiamo scrivere delle espressioni di calcolo del tipo:
z=3*4*sqrt(56)-doppio(5);
oppure
z=3+doppio(sqrt(45));
in questo caso il risultato della radice sqrt (che è una funzione non void) viene usato come parametro attuale della funzione doppio.
I parametri attuali possono essere specificati attraverso delle costanti, delle singole variabili o delle espressioni di calcolo (nella realtà le costanti e le singole variabili sono le forme più semplici di una espressione di calcolo). Allora possiamo anche scrivere:
z= 1+doppio( doppio(3));
oppure
z= doppio( 10 + doppio ( sqrt(4) )) +22;
ora z=50 cioè si comportano come le espressioni matematiche che utilizziamo di solito.
le funzioni void non possono invece essere inserite in espressioni di calcolo, cioè se
void doppio ( float *n)
{ *n= *n*2;
}
non posso scrivere
float a=4;
z=doppio( &a)+7;
ma invece
float a=4;
doppio( &a);
z=a+7;
Funzioni Ricorsive
[modifica]Le funzioni (void e non void) possono essere richiamate non solo da altre funzioni ma anche all'interno della funzione stessa, in questo caso si parla di funzioni ricorsive ( che cioè richiamano se stesse)
Un tipico esempio è il calcolo del fattoriale, in matematica il fattoriale del numero n si indica con il simbolo n! e per calcolarlo si seguono le seguenti regole
NB con n si intende un numero naturale 0,1,2,3,4,....
se n=0 allora n!=1 cioè 0!=1 se n>0 allora n!= n* (n-1)!
quindi 3!= 3* 2! = 3* 2 *1!= 3*2*1*0!= 3*2*1*1 = 6
si noti la particolare definizione del fattoriale il fattoriale del numero n è uguale a n moltiplicato per il fattoriale di n-1 in cui non spiego esattamente come calcolare il fattoriale, ma dico solo che per calcolare il fattoriale di n devo saper fare il fattoriale di n-1 , quindi spiego il fattoraile in funzione di se stesso (ecco la ricorsività); e poi per poter fare effettivamente il calcolo devo completare la spiegazione con una condizione di terminazione se n è uguale a zero allora il fattoriale vale 1
Tutti i problemi ricorsivi (come pure le soluzioni dei problemi ricorsivi) hanno 2 elementi
- una definizione/espressione ricorsiva (in cui spiego una cosa in funzione di se stessa)
- e una condizione di terminazione
se vogliamo scrivere una funzione ricorsiva per il calcolo dell' n! scriviamo
long fattoriale (long n)
{ if(n==0)
return 1;
else
return n*fattoriale(n-1);
}
se richiamo la funzione con
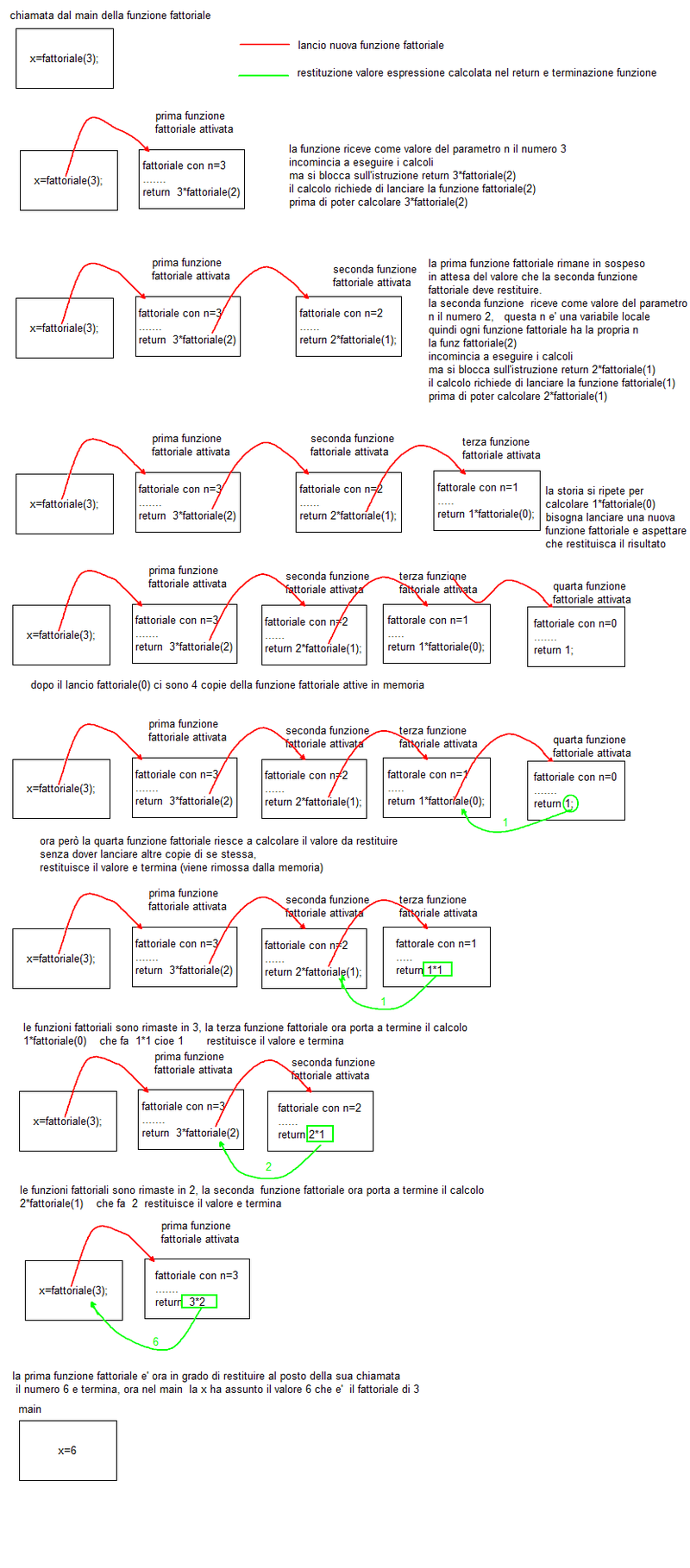
z=fattoriale(3);
succede che si attiva il codice della funzione fattoriale(3) che si ferma nel calcolo di return 3*fattoriale(2) si ferma perché deve ottenere il risultato della chiamata alla funzione fattoriale(2)
a questo punto si attiva una copia del codice della funzione fattoriale con valore di n=2 questa funzione fattoriale(2) si ferma pure lei nel calcolo di
return 2*fattoriale(1) che richiede l'esecuzione della funzione fattoriale(1)
in memoria si forma una terza copia del codice della funzione fattoriale con un valore n=1 (attenzione ogni funzione fattoriale ha una propria variabile locale di nome n con valori diversi) che si ferma nel calcolo return 1*fattoriale(0) perché in attesa del risultato della chiamata alla funzione fattoriale(0)
ora in memoria si crea una quarta copia della funzione rivolta al calcolo del fattoriale(0), in questo caso si attiva la condizione di terminaziome e return restituisce il valore 1 al precedente fattoriale (a questo punto la quarta copia del codice essendo la funzione terminata viene rimossa dalla memoria
ora la terza copia della funzione che ha ricevuto il risultato del fattoriale di zero può terminare il calcolo return 1*fattoriale(0) che restituisce il valore 1 (la terza copia del fattoriale termina e viene rimossa dalla memoria ora la seconda copia della funzione che ha ricevuto il risultato del fattoriale di uno può terminare il calcolo return 2*fattoriale(1) che restituisce 2 (la seconda copia del fattoriale termina e viene rimossa dalla memoria) ora la prima copia della funzione che ha ricevuto il risultato del fattoriale di due può terminare il calcolo return 3*fattoriale(2) che restituisce 6 (la prima copia del fattoriale termina e viene rimossa dalla memoria) ora z=fattoriale(3) riceve il valore del fattoriale(3) che vale 6 e lo assegna alla variabile z
Quindi nell'uso delle funzioni ricorsive c'è una fase di espansione in cui si creano più copie della funzione ricorsiva e una fase di contrazione del numero di copie della funzione ricorsiva che parte quando si raggiunge la condizione di terminazione e termina quando si riesce a calcolare l'espressione iniziale.
Alcuni problemi di natura ricorsiva sono risolvibili semplicemente usando delle funzioni ricorsive, problemi di natura ricorsiva possono essere risolti anche non ricorsivamente, ma di solito con struttura risolutiva più complicata anche se più, veloce (caso quicksort).
Passaggio dei parametri alle funzioni
[modifica]Quando si utilizza una funzione possono essere passati anche degli array, il passaggio di un array (vettore,matrice etc) avviene sempre per indirizzo, la copia dei valori di un array (dal parametro attuale a quello formale) viene infatti considerata una operazione troppo onerosa, questo comporta che quando passiamo l'indirizzo di un vettore o di una matrice permettiamo alla funzione chiamata tramite i puntatori di cambiare i valori nelle celle di memoria della matrice passata. Ricordatevi inoltre che il passaggio dei parametri rallenta l'esecuzione del codice, per velocizzare al massimo una funzione possiamo usare le variabili globali.
I puntatori essendo fonte di errore tendono ad essere nei linguaggi di programmazione moderni sostituiti/nascosti da una sintassi semplificata che permette però di ottenere lo stesso risultato.
per passare un vettore di n elementi allora possiamo
dimensione vettore parametro formale uso parametro formale nella funzione parametro attuale costante (esempio=10) int v[10] v[2]=7; vett variabile k int v[], int n v[2]=7; vett,k variabile k int *p , int n *(p+2)=7; vett,k
per passare una matrice di nr*nc elementi allora possiamo
dimensione matrice parametro formale uso parametro formale nella funzione parametro attuale
riga e colonna costanti 4*6 int m[4][6] m[2][3]=7; mat
riga var colonna costante 6 int m[][6], int nr m[2][3]=7; mat,nr
riga e col variabili int *p , int nr, int nc *(p+2*nc+3)=7; (int *) mat,nr,nc
o per elemento i,j *(p+i*nc+j)=7;
una variabile singola può essere passata per valore ,per indirizzo o per reference
parametro formale uso parametro formale nella funzione parametro attuale per valore int z k=z+4; 5/ a / 3*a per indirizzo int *p *p=6; &a per reference int &k k=7 a
il passaggio per reference è un passaggio per indirizzo con sintassi semplificata , scrivendo il nome della variabile passo il suo indirizzo, il parametro attuale davanti al nome ha il simbolo & per ricordare che il passaggio è per reference, la variabile formale (che nasconde internamente il puntatore) viene usata normalmente e tutto quello che le succede si riflette sulla variabile attuale